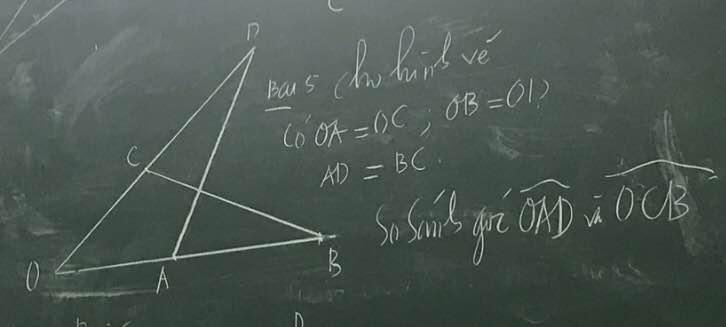Xét ΔACB và ΔBDA có:
AC=BD(gt)
CB=DA(gt)
chung AB
⇒ΔACB = ΔBDA (c.c.c)
⇒\(\widehat{BAC}=\widehat{ABD}\) (2 góc tương ứng)
Mà 2 góc này lại so le trong nên AC//BD
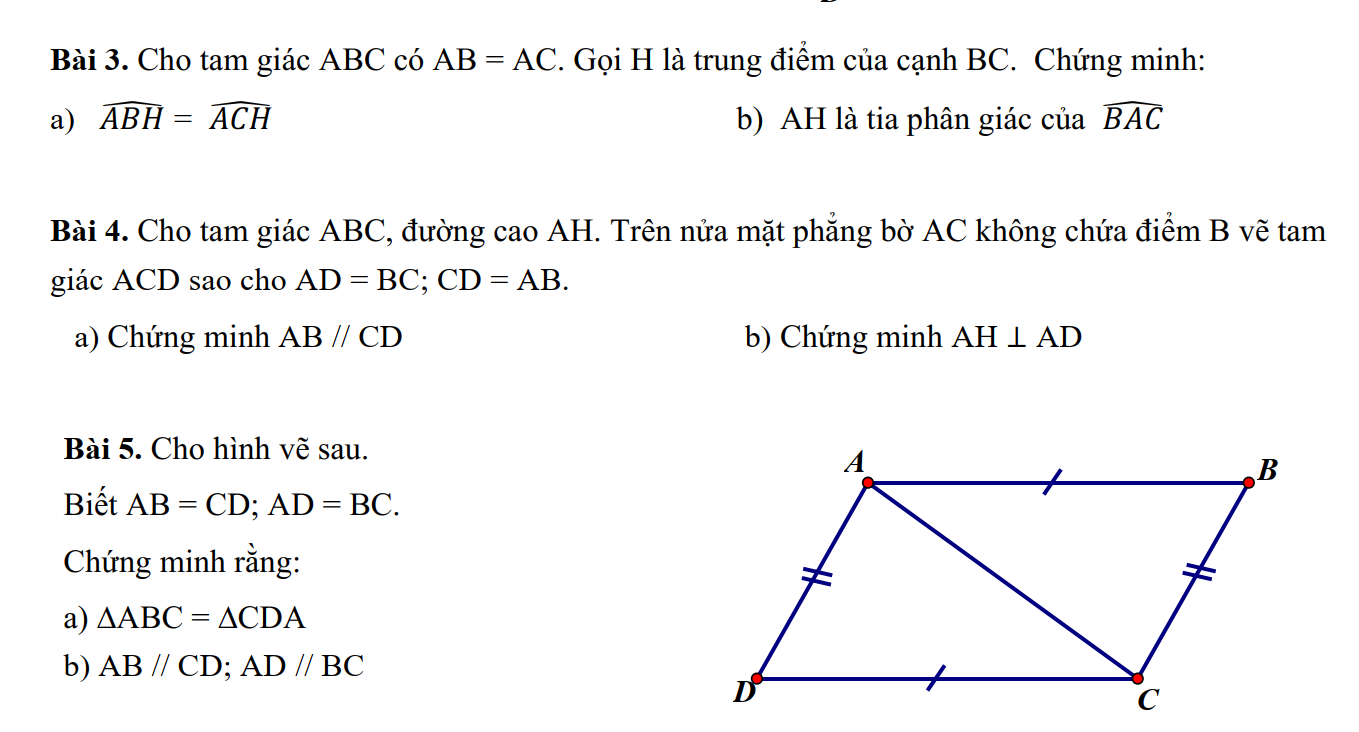
Xét tam giác ABC và tam giác BAD có:
AC=BD( gt)
BC=AD( gt)
AB chung
=> △ABC=△BAD( c.c.c)
=> \(\widehat{ABC}=\widehat{BAD}\) (2 góc tương ứng)
Mà 2 góc này là 2 góc so le trong
=> AC//BD
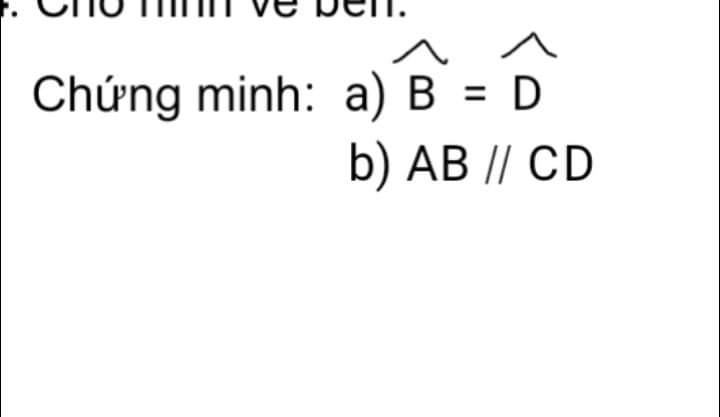
Xét ΔACB và ΔBDA có
AC=BD
CB=DA
AB chung
Do đó: ΔACB=ΔBDA
Suy ra: \(\widehat{CAB}=\widehat{DBA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD