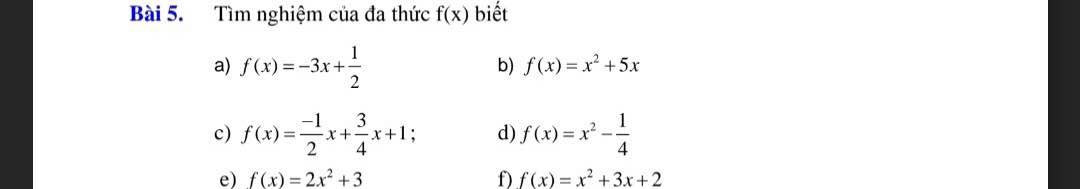`a)f(x)=0<=>-3x+1/2=0<=>-3x=-1/2<=>x=1/6` $\\$ `b)f(x)=0<=>x^2+5x=0<=>x(x+5)=0<=>` \(\left[ \begin{array}{l}x=0\\x=-5\end{array} \right.\) $\\$ `c)f(x)=0<=>-1/2x+3/4x+1=0<=>1/4x+1=0<=>1/4x=-1<=>x=-4` $\\$ `d)f(x)=0<=>x^2-1/4=0<=>x^2=1/4<=>` \(\left[ \begin{array}{l}x=\dfrac12\\x=-\dfrac12\end{array} \right.\) $\\$ `e)f(x)=0<=>2x^2+3=0<=>2x^2=-3<=>x^2=-3/2` vô lý vì `x^2>=0` $\\$ `f(x)=0<=>x^2+3x+2=0<=>x^2+x+2x+2=0<=>x(x+1)+2(x+1)=0<=>(x+1)(x+2)=0<=>` \(\left[ \begin{array}{l}x=-2\\x=-1\end{array} \right.\)
a) Đặt f(x)=0
\(\Leftrightarrow-3x+\dfrac{1}{2}=0\)
\(\Leftrightarrow-3x=-\dfrac{1}{2}\)
hay x=6
b) Đặt f(x)=0
\(\Leftrightarrow x^2+5x=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
c) Đặt f(x)=0
\(\Leftrightarrow\dfrac{-1}{2}x+\dfrac{3}{4}x+1=0\)
\(\Leftrightarrow\dfrac{1}{2}x=-1\)
hay x=-2
d) Đặt f(x)=0
\(\Leftrightarrow x^2-\dfrac{1}{4}=0\)
\(\Leftrightarrow x^2=\dfrac{1}{4}\)
hay \(x\in\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
e) Đặt f(x)=0
\(\Leftrightarrow2x^2+3=0\)
\(\Leftrightarrow2x^2=-3\)(vô lý)
Vậy: \(x\in\varnothing\)
f) Đặt f(x)=0
\(\Leftrightarrow x^2+3x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)