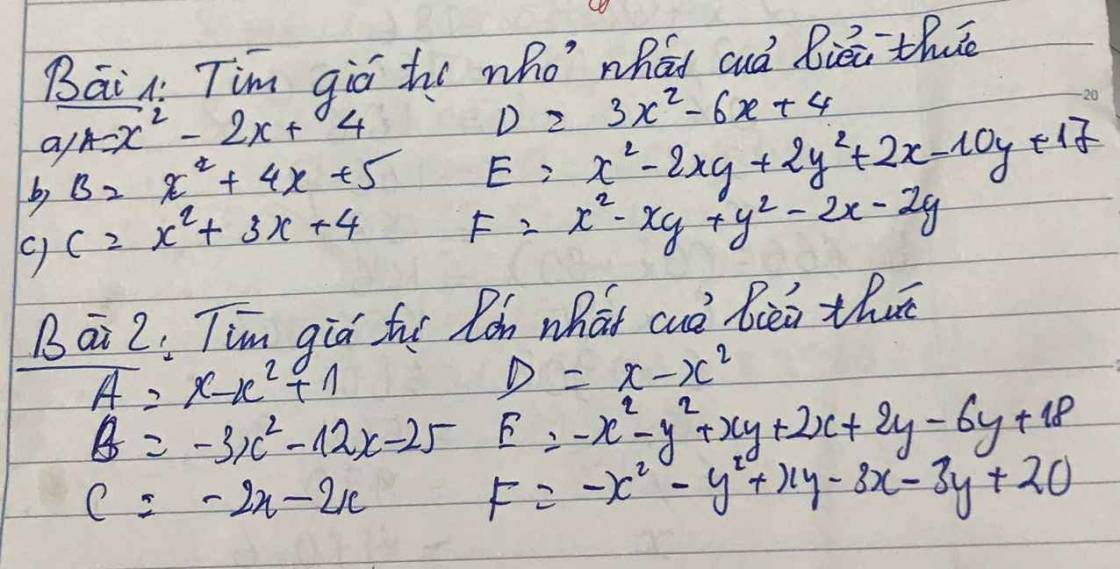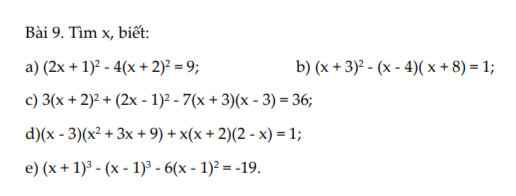giúp mik với
a: A=(2-1)(2+1)(2^2+1)*...*(2^64+1)+1
=(2^2-1)(2^2+1)(2^4+1)*...*(2^64+1)+1
=(2^4-1)(2^4+1)*(2^8+1)*...(2^64+1)+1
=(2^8-1)(2^8+1)(2^16+1)(2^32+1)(2^64+1)+1
...
=2^128-1+1=2^128
b: \(B=\dfrac{1}{2}\left[\left(3-1\right)\left(3+1\right)\cdot...\cdot\left(3^{64}+1\right)+2\right]\)
\(=\dfrac{1}{2}\left[\left(3^2-1\right)\left(3^2+1\right)\cdot...\cdot\left(3^{64}+1\right)+2\right]\)
\(=\dfrac{1}{2}\left[3^{128}-1+2\right]=\dfrac{3^{128}+1}{2}\)
c: \(=\left(a+b\right)^2+2c\left(a+b\right)+c^2+\left(a+b\right)^2-2c\left(a+b\right)+c^2-2\left(a+b\right)^2\)
=2c^2
Đúng 1
Bình luận (0)
