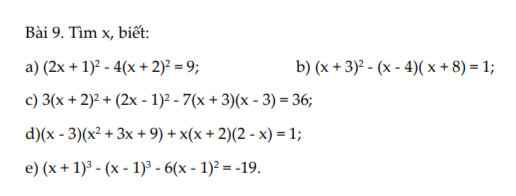1
a
\(A=x^2-2x+4=x^2-2x+1+3\\=\left(x-1\right)^2+3\ge3\)
Min A = 3 khi và chỉ khi `x=1`
b
\(B=x^2+4x+5=x^2+4x+4+1\\ =\left(x+2\right)^2+1\ge1\)
Min B = 1 khi và chỉ khi `x=-2`
c
\(C=x^2+3x+4=x^2+3x+\dfrac{9}{4}+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
Min C = \(\dfrac{7}{4}\) khi và chỉ khi \(x=-\dfrac{3}{2}\)
d
\(D=3x^2-6x+4=3\left(x^2-2x+\dfrac{4}{3}\right)\\ =3\left(x^2-2x+1+\dfrac{1}{3}\right)\\ =3\left(x-1\right)^2+3.\dfrac{1}{3}\ge3.\dfrac{1}{3}\)
Min D = 1 khi và chỉ khi `x=1`

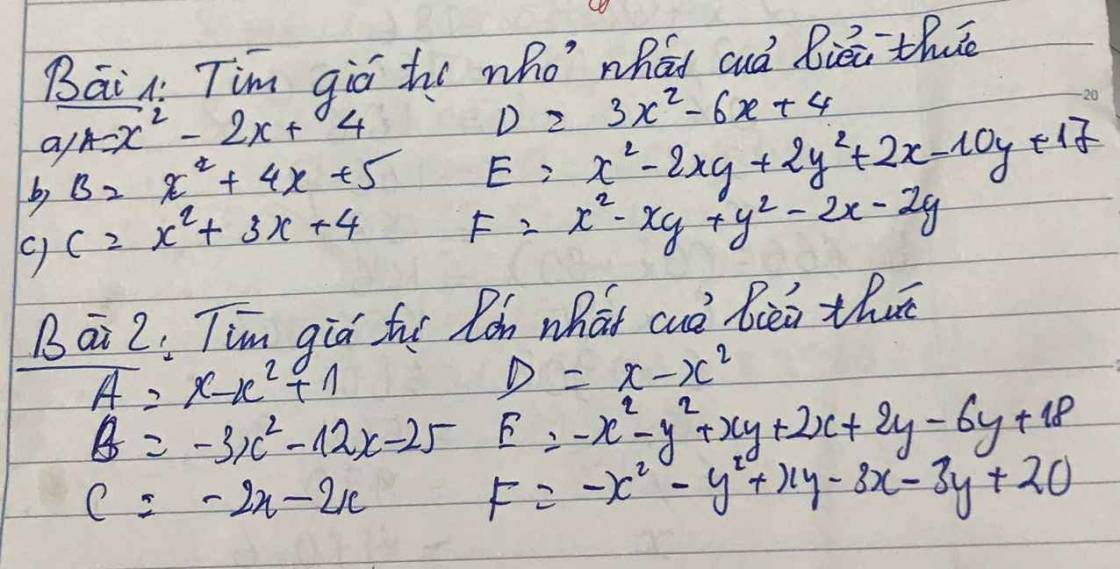








 giúp mik với
giúp mik với

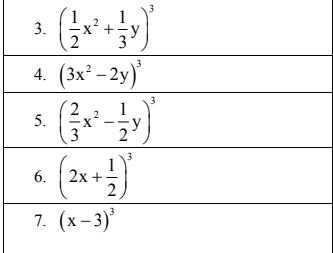 Ai giúp e 5 câu nay` đc không ạ ! e cmơn trước ạ :)))
Ai giúp e 5 câu nay` đc không ạ ! e cmơn trước ạ :)))