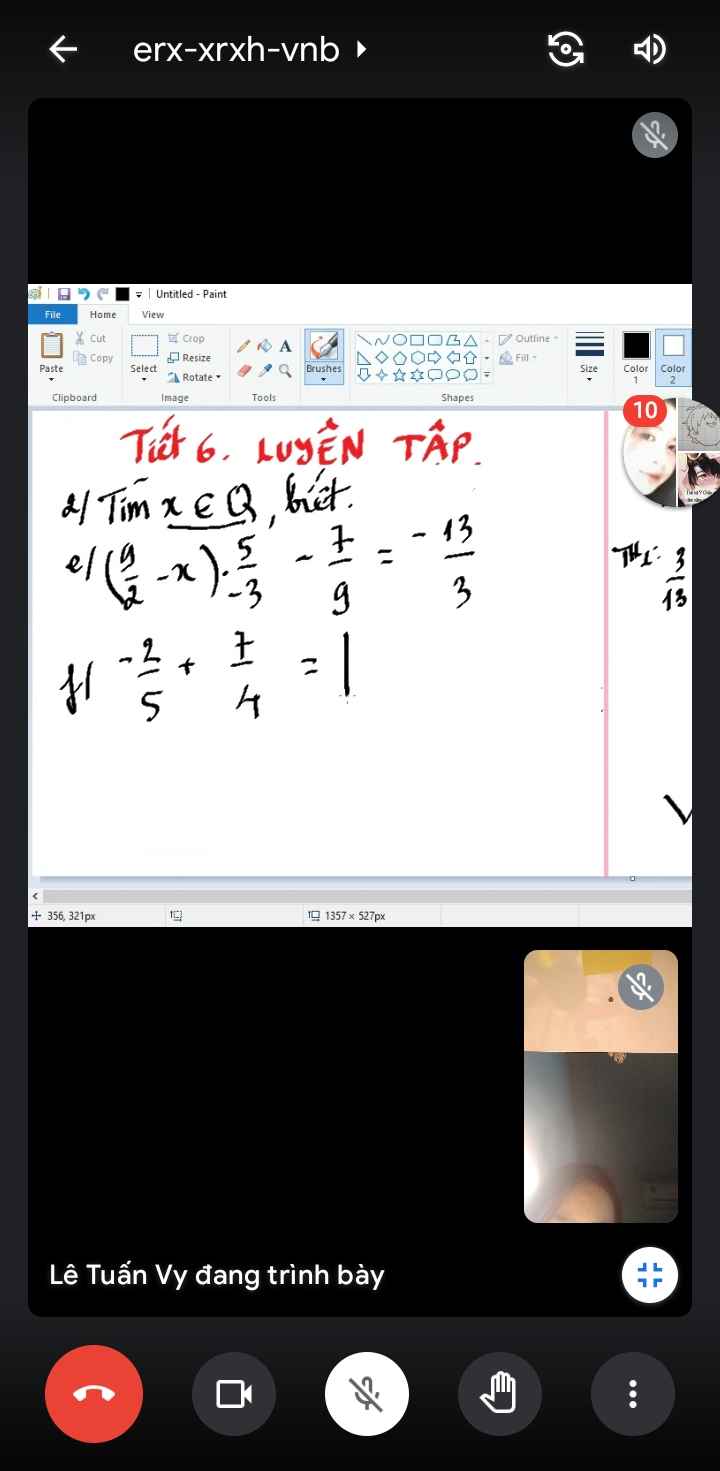
\(3^{x-2015}=\dfrac{1}{243}\)
=>\(3^{x-2015}=3^{-5}\)
=>x-2015=-5
=>x=2010
\(3^{x-2015}=\dfrac{1}{243}=3^{-5}\\ Nên:x-2015=-5\\ Vậy:x=-5+2015=2010\)
`3^(x-2015)=1/243`
`=>3^(x-2015)=3^(-5)`
`=>x-2015=-5`
`=>x=-5+2015`
`=>x=2010`
Vậy `x=2010`
\(3^{x-2015}=\dfrac{1}{243}\)
\(\Rightarrow3^{x-2015}=1:3^5\)
\(\Rightarrow3^{x-2015}=3^{-5}\)
\(\Rightarrow x-2015=-5\)
\(\Rightarrow x=-5+2015\)
\(\Rightarrow x=2010\)
Vậy: \(x=2010\).

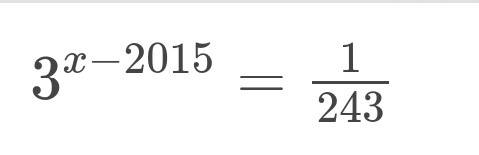 giúp em với ạ
giúp em với ạ








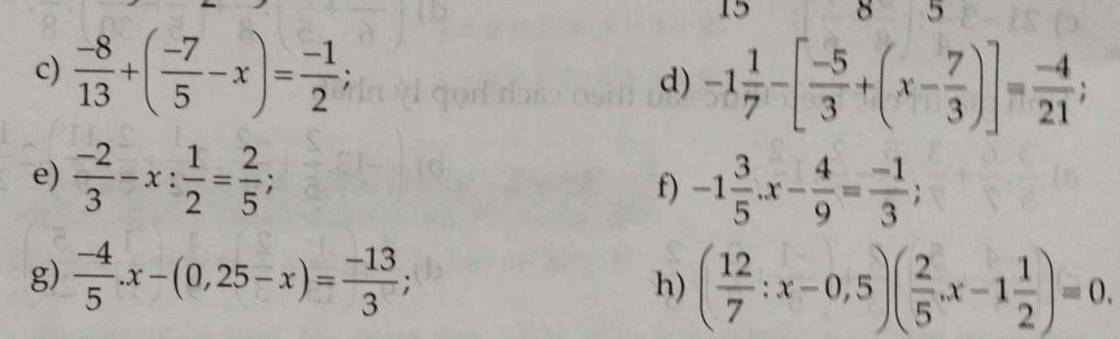

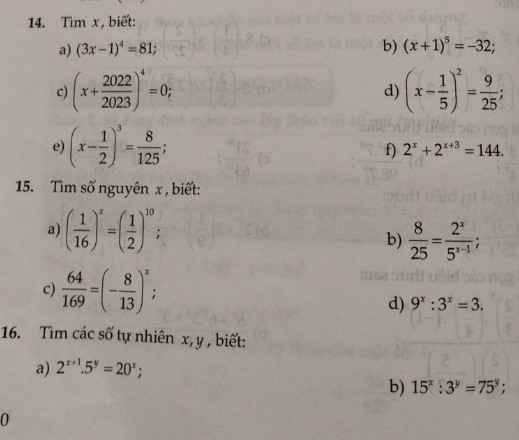

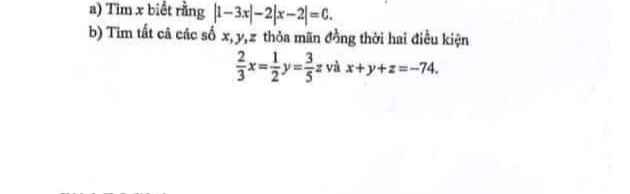

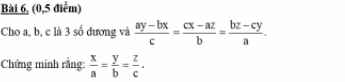 Giúp em với ạ
Giúp em với ạ