14:
a) \(\left(3x-1\right)^4=81\)
\(\Rightarrow\left(3x-1\right)^4=\left(\pm3\right)^4\)
\(\Rightarrow\left[{}\begin{matrix}3x-1=3\\3x-1=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3x=4\\3x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
b) \(\left(x+1\right)^5=-32\)
\(\Rightarrow\left(x+1\right)^5=\left(-2\right)^5\)
\(\Rightarrow x+1=-2\)
\(\Rightarrow x=-3\)
c) \(\left(x+\dfrac{2022}{2023}\right)^3=0\)
\(\Rightarrow x+\dfrac{2022}{2023}=0\)
\(\Rightarrow x=-\dfrac{2022}{2023}\)
d) \(\left(x-\dfrac{1}{5}\right)^2=\dfrac{9}{25}\)
\(\Rightarrow\left(x-\dfrac{1}{5}\right)^2=\left(\dfrac{3}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{5}=\dfrac{3}{5}\\x-\dfrac{1}{5}=-\dfrac{3}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
e) \(\left(x-\dfrac{1}{2}\right)^3=\dfrac{8}{125}\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{2}{5}\right)^3\)
\(\Rightarrow x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(\Rightarrow x=\dfrac{9}{10}\)
f) \(2^x+2^{x+3}=144\)
\(\Rightarrow2^x\cdot\left(1+2^3\right)=144\)
\(\Rightarrow2^x\cdot9=144\)
\(\Rightarrow2^x=16\)
\(\Rightarrow2^x=2^4\)
\(\Rightarrow x=4\)
16:
a: \(\Leftrightarrow2^{x+1}\cdot5^y=\left(2^2\cdot5\right)^x=2^{2x}\cdot5^x\)
=>2x=x+1 và x=y
=>x=1=y
b: \(\Leftrightarrow5^x\cdot3^{x-y}=3^y\cdot5^{2y}\)
=>x=2y và x-y=y
=>x=2y(luôn đúng)
Vậy: \(\left(x,y\right)\in N\)

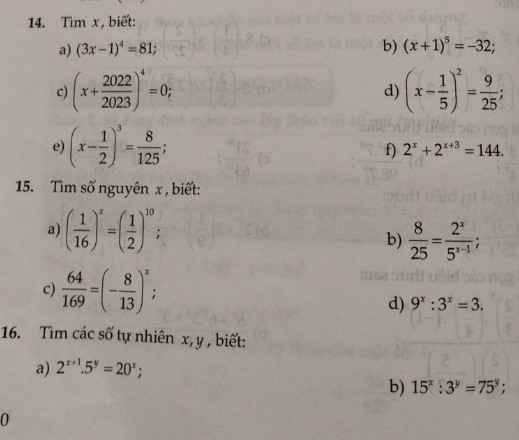








 Giúp em với . Em cảm ơn nhiều
Giúp em với . Em cảm ơn nhiều