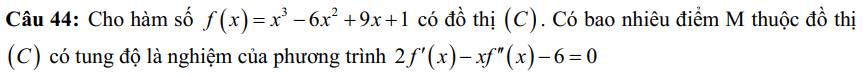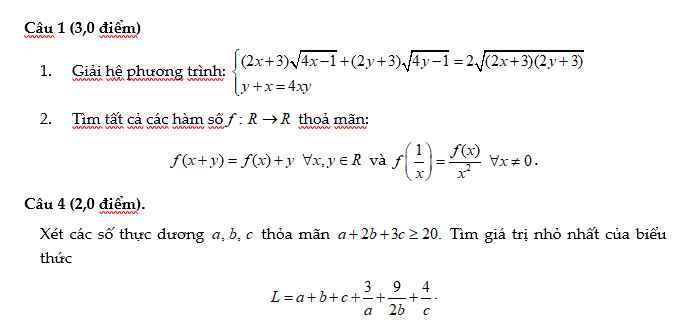46.
\(y'=2cos2x+2sin2x\)
\(y'=sin4x+2m+1\Leftrightarrow2cos2x+2sin2x=sin4x+2m+1\)
\(\Leftrightarrow2m=2cos2x+2sin2x-sin4x-1\)
Đặt \(sin2x+cos2x=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow t^2-1=2sin2x.cos2x=sin4x\)
\(\Rightarrow2m=2t-\left(t^2-1\right)-1=2t-t^2\)
Ta có: \(f\left(t\right)=2t-t^2=1-\left(t-1\right)^2\le1\)
\(f\left(-\sqrt{2}\right)=-2-2\sqrt{2}\) ; \(f\left(\sqrt{2}\right)=-2+2\sqrt{2}\)
\(\Rightarrow-2-2\sqrt{2}\le f\left(t\right)\le1\)
\(\Rightarrow-2-2\sqrt{2}\le2m\le1\)
\(\Rightarrow-1-\sqrt{2}\le m\le\dfrac{1}{2}\)
44.
\(f'\left(x\right)=3x^2-12x+9\)
\(f''\left(x\right)=6x-12\)
\(2f'\left(x\right)-x.f''\left(x\right)-6=0\)
\(\Leftrightarrow2\left(3x^2-12x+9\right)-x\left(6x^2-12\right)-6=0\)
\(\Leftrightarrow x=1\)
\(\Rightarrow x^3-6x^2+9x+1=1\)
\(\Rightarrow x\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Có 2 điểm thỏa mãn
45.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân \(\Rightarrow\) có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-1\)
\(\Rightarrow\left(x-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
\(y\left(3\right)=3\) ; \(y\left(-1\right)=-1\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-3\right)+3=-x+6\\y=-\left(x+1\right)-1=-x-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a+b=5\\a+b=-3\end{matrix}\right.\)
47.
\(g'\left(x\right)=\left(2x+2\right).f'\left(x^2+2x-m\right)\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\f'\left(x^2+2x-m\right)=0\end{matrix}\right.\)
\(f'\left(x^2+2x-m\right)=0\Rightarrow\left[{}\begin{matrix}x^2+2x-m=1\\x^2+2x-m=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+2x-m-1=0\\x^2+2x-m-2=0\end{matrix}\right.\) (1)
Pt \(f'\left(x\right)=0\) có nhiều nghiệm nhất khi 2 pt (1) đều có 2 nghiệm pb và khác -1
\(\Rightarrow\left\{{}\begin{matrix}-m-2\ne0\\-m-3\ne0\\m+2>0\\m+3>0\end{matrix}\right.\) \(\Rightarrow m>-2\)
\(\Rightarrow20-\left(-1\right)+1=22\) giá trị nguyên
48.
\(\sqrt{2x^2+mx-1}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\2x^2+mx-1=\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x^2+\left(m+2\right)x-2=0\end{matrix}\right.\)
\(\Rightarrow-\left(m+2\right)=\dfrac{x^2-2}{x}\)
\(f\left(x\right)=\dfrac{x^2-2}{x}\) đồng biến khi \(x\ge1\) có \(f\left(1\right)=-1\)
\(\Rightarrow\) Pt có nghiệm khi \(-\left(m+2\right)\ge-1\)
\(\Rightarrow m\le-1\)
\(\Rightarrow2024\) giá trị m nguyên