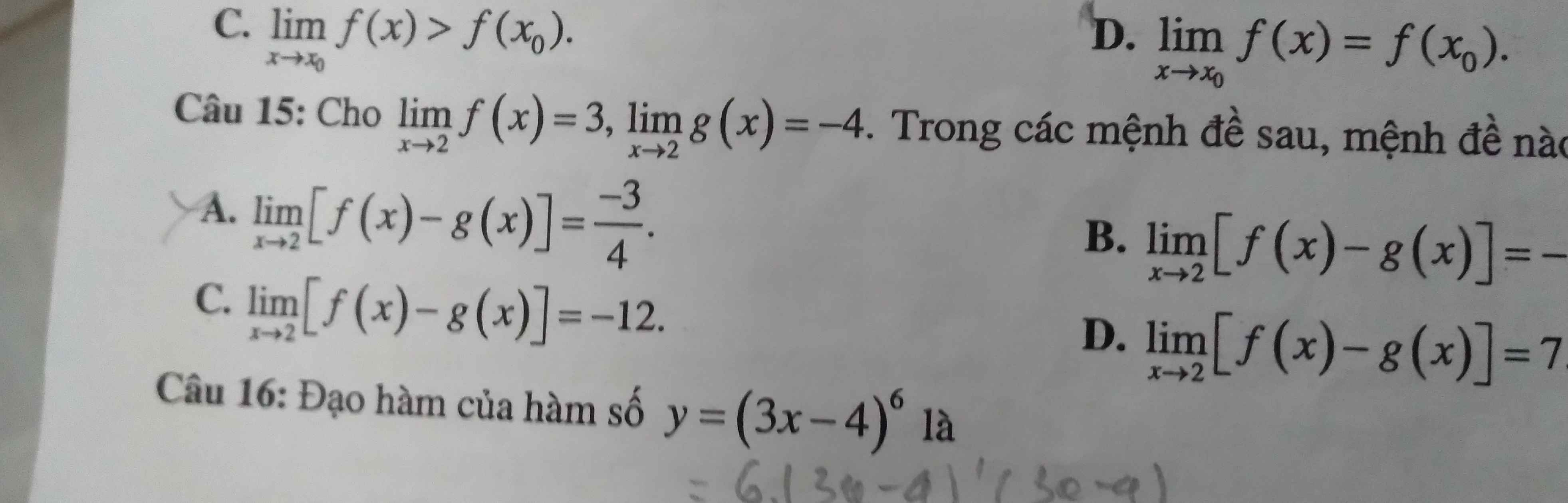Question

Giúp e câu 1 đến 6 đi ạ

Answer 1

1:

\(y'=\dfrac{\left(x-1\right)'\left(x+2\right)-\left(x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)

f(-1)=(-1-1)/(-1+2)=-2

f'(-1)=3/(-1+2)^2=3

y-f(-1)=f'(-1)(x+1)

=>y+2=3(x+1)=3x+3

=>y=3x+1

2: y'=2x+3

f(1)=1+3-2=2

f'(1)=2+3=5

y-f(1)=f'(1)(x-1)

=>y-2=5(x-1)=5x-5

=>y=5x-3

4: y=3

=>x^2+2x+4=3

=>x^2+2x+1=0

=>x=-1

y=x^2+2x+4

=>y'=2x+2=f'(x)

f'(-1)=-2+2=0

y-f(-1)=f'(-1)(x+1)

=>y+3=0(x+1)

=>y=-3