Ôn tập toán 8
Các câu hỏi tương tự
giải bất phương trình
\(\frac{1}{2x-3}\)-\(\frac{3}{x\left(2x-3\right)}\)=\(\frac{5}{x}\)
Giải các bất phương trình sau và biểu diễn nghiệm trên trục số
a, 2x + 3(x – 2) < 5x – (2x – 4).
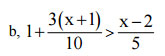
Giải bất phương trình, biểu diễn tập nghiệm trên trục số
\(\frac{4x-5}{3}>\frac{7-x}{5}p\)
các bạn xem lại đề, không biết mình đánh có đúng không nữa
\(A=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2015}-\frac{1}{2016}+\frac{1}{2017}\)
\(B=\frac{1}{1009}+\frac{1}{1010}+...+\frac{1}{2016}+\frac{1}{2017}\)
Tính \(\left(A-B\right)^{2016^{2017}}\)
Giải bất phương trình sau: 3.(2x2+5) _> 6x (x+5)
[Lớp 8]Bài 1. Giải phương trình sau đây:a) 7x+121;b) left(4x-10right)left(24+5xright)0;c) left|x-2right|2x-3;d) dfrac{x+2}{x-2}-dfrac{1}{x}dfrac{2}{xleft(x-2right)}. Bài 2. Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số: dfrac{x-1}{3}-dfrac{3x+5}{2}ge1-dfrac{4x+5}{6}. Bài 3. Tìm giá trị lớn nhất của A-x^2+2x+9. Bài 4. Giải bài toán bằng cách lập phương trình:Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện ngư...
Đọc tiếp

[Lớp 8]
Bài 1. Giải phương trình sau đây:
a) \(7x+1=21;\)
b) \(\left(4x-10\right)\left(24+5x\right)=0;\)
c) \(\left|x-2\right|=2x-3;\)
d) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}.\)
Bài 2. Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số:
\(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}.\)
Bài 3. Tìm giá trị lớn nhất của \(A=-x^2+2x+9.\)
Bài 4. Giải bài toán bằng cách lập phương trình:
Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện người đó giảm vận tốc 6km/h nên đã đến B chậm hơn dự định là 24 phút.
Tính quãng đường AB.
Bài 5. Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD⊥ AB (D ∈ AB), HE ⊥ AC (E∈ AC). AB=12cm, AC=16cm.
a) Chứng minh: ΔHAC đồng dạng với ΔABC;
b) Chứng minh AH2=AD.AB;
c) Chứng minh AD.AB=AE.AC;
d) Tính \(\dfrac{S_{ADE}}{S_{ABC}}.\)
1.Giải phương trình: \(\frac{1}{x^2+9x+20}+\frac{1}{x^2+11x+30}+\frac{1}{x^2+13x+42}=\frac{1}{18}\)
2.Giải phương trình: \(8\left(x+\frac{1}{x}\right)^2+4\left(x^2+\frac{1}{x^2}\right)^2-4\left(x^2+\frac{1}{x^2}\right)\left(x+\frac{1}{x}\right)^2=\left(x+4\right)^2\)
Giải phương trình sau:\(\frac{2-x}{2007}-1=\frac{1-x}{2008}-\frac{x}{2009}\)
Tinh: \(\frac{2^{2016}+2^{2016}}{-2^{2017}}\)









