Tam giác đồng dạng
Các câu hỏi tương tự
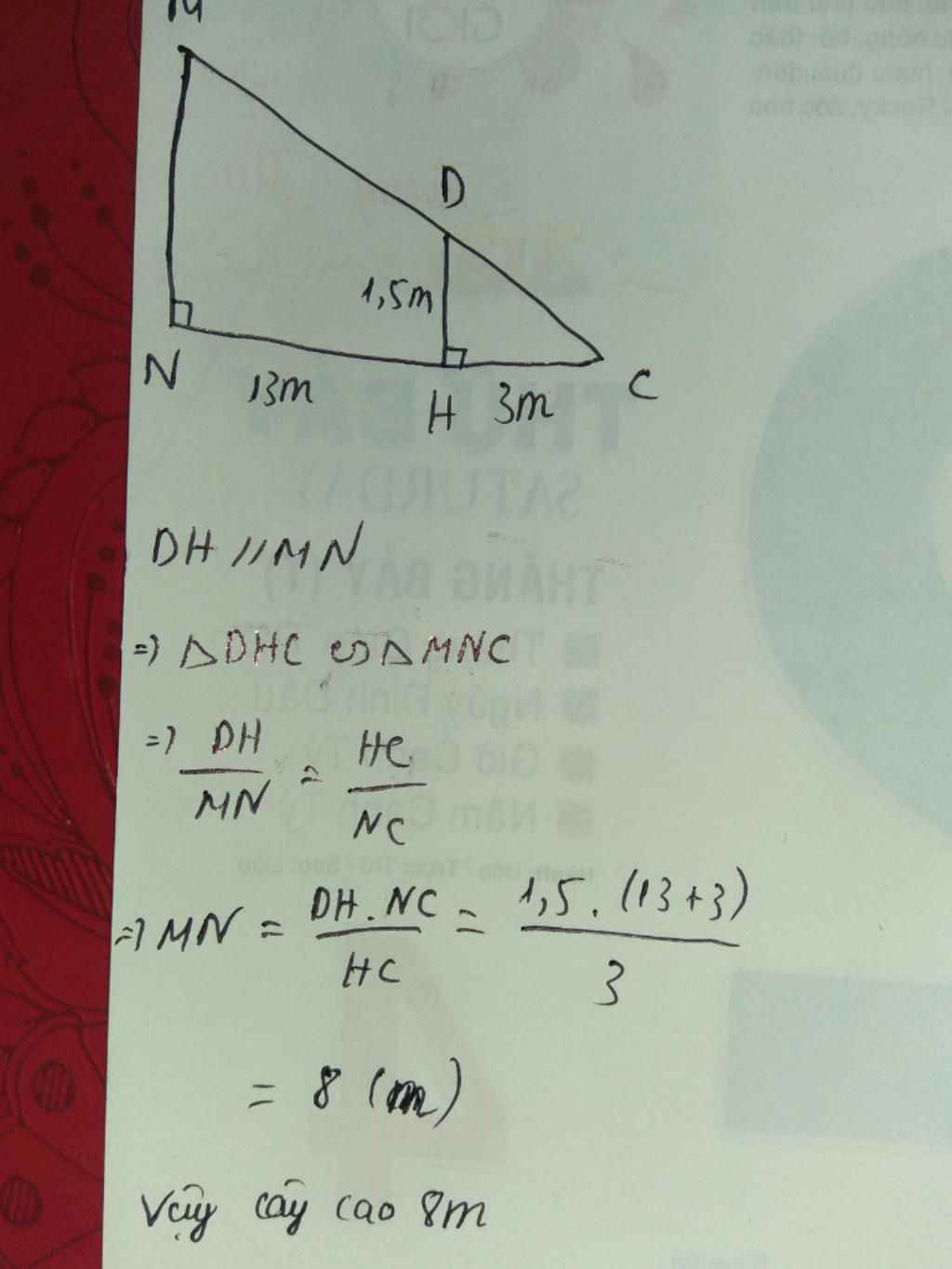
Một người đứng ở vị trí A cách một cái cây 10m. Để đo chiều cao cây, người đó đựng 1 cái cọc có chiều dài 2m ở vị trí mà từ A có thể nhìn thẳng qua đỉnh cọc tới đỉnh ngọn cây. Đo khoảng cách từ A đến cái chân cọc ở vị trí B là 4m. Hãy tính chiều cao của cây theo cách người đó làm.
Giúp em với ạ !
Cách xác định khoảng cách giữa điểm trên thưc tế hoặc chiều cao của vật mà ta không thể tới nơi để đo đạc
Cho hình chữ nhật có AB > BC. Gọi H là chân đường cao hạ từ A xuống BD.
a) Chứng minh AD2 = DH.DB
b) Chứng minh tam giác AHD đồng dạng với tam giác ABC
c) Gọi M và N lần lượt là trung điểm của DH và BC. Chứng minh học MAD bằng góc NAC.
d) Tính số đo góc AMN
Bóng của 1 cây trên mặt đất có độ dài là 15m, cùng thời điểm đó một thanh sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1m. Tính chiều dài của cây?
Cho ΔMNP vuông tại M, đường cao MH. Gọi D là điểm tùy ý trên cạnh MN, đường thẳng qua H và vuông góc với HD, cắt MP tại E. Tìm vị trí của D trên cạnh MN để ΔDHE có diện tích nhỏ nhất.
N M P H D E
cho ▲ABC vuông tại A , có AM là trung tuyến , đường cao AH . trên cùng nữa mặt phẳng bờ BC có chứa điểm A vẻ 2 tia x ,Cy cùng vuông góc với BC . qua A kẻ đường thẳng vuông góc với AM , cắt Bx và Cy lần lượt tại P và Q . chứng minh :
a) APBP và AQCQ
b) PC là trung điểm của AH
c) khi BC cố định BC2a , điểm A chuyển động sao cho góc BAC bằng 90 độ .tìm vị trí của điểm H trên đoạn thẳng BC để diện tích ▲ABH đạt giá trị lớn nhất . tìm giá trị lớn nhất đó
Đọc tiếp
cho ▲ABC vuông tại A , có AM là trung tuyến , đường cao AH . trên cùng nữa mặt phẳng bờ BC có chứa điểm A vẻ 2 tia x ,Cy cùng vuông góc với BC . qua A kẻ đường thẳng vuông góc với AM , cắt Bx và Cy lần lượt tại P và Q . chứng minh :
a) AP=BP và AQ=CQ
b) PC là trung điểm của AH
c) khi BC cố định BC=2a , điểm A chuyển động sao cho góc BAC bằng 90 độ .tìm vị trí của điểm H trên đoạn thẳng BC để diện tích ▲ABH đạt giá trị lớn nhất . tìm giá trị lớn nhất đó
2 : Cho phươngtrình ẩn x: ( m-1)x + m2 – 1 0 (1)
a. Giải phươngtrình (1) khi m 2
b. Tìm giá trị của m sao cho phươngtrình (1) nhận x 3 làm nghiệm
3: Một phânsố có tử số bé hơn mẫu số là 11. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phânsố bằng 3/4 . Tìm phânsố ban đầu?
4 Cho tam giác ABC vuông tại A, đường cao AH, HB 4cm, HC 9 cm. Kẻ HD ⊥ AB;
HE ⊥ AC
a) Chứng minh ΔABH ∼ ΔCAH
b) Tính độ dài đoạn thẳng DE.
c) Các đường thẳng vuông góc với DE tại D và E cắt B...
Đọc tiếp
2 : Cho phươngtrình ẩn x: ( m-1)x + m2 – 1 = 0 (1)
a. Giải phươngtrình (1) khi m = 2
b. Tìm giá trị của m sao cho phươngtrình (1) nhận x = 3 làm nghiệm
3: Một phânsố có tử số bé hơn mẫu số là 11. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phânsố bằng 3/4 . Tìm phânsố ban đầu?
4 Cho tam giác ABC vuông tại A, đường cao AH, HB = 4cm, HC = 9 cm. Kẻ HD ⊥ AB;
HE ⊥ AC
a) Chứng minh ΔABH ∼ ΔCAH
b) Tính độ dài đoạn thẳng DE.
c) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N. Tính diện tích tứ giác DENM ?
Mình đã sửa lại đề. Bạn Hung nguyen phát hiện ra lỗi sai và được tặng 2GP.
Có vẻ hơi khó nhỉ ? Cho 4GP nhé.
Chuyên mục toán vui vui !
Chứng minh rằng Delta ABC đồng dạng với một tam giác có ba cạnh lần lượt bằng NGHỊCH ĐẢO độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Đọc tiếp
Mình đã sửa lại đề. Bạn Hung nguyen phát hiện ra lỗi sai và được tặng 2GP.
Có vẻ hơi khó nhỉ ? Cho 4GP nhé.
Chuyên mục toán vui vui !
Chứng minh rằng \(\Delta ABC\) đồng dạng với một tam giác có ba cạnh lần lượt bằng NGHỊCH ĐẢO độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Cho tam giác ABC cân tại A, đường cao AH. Gọi M là trung điểm của AC; gọi D là điểm đối xứng với H qua M.
a) CM tứ giác AHCD là hình chữ nhật.
b) Tìm điều kiện của ΔABC để tứ giác AHCD là hình vuông
c) Tính diện tích tứ giác AHCD khi biết diện tích ΔABC là 10cm2