Mình đã sửa lại đề. Bạn Hung nguyen phát hiện ra lỗi sai và được tặng 2GP.
Có vẻ hơi khó nhỉ ? Cho 4GP nhé.
Chuyên mục toán vui vui !
Chứng minh rằng \(\Delta ABC\) đồng dạng với một tam giác có ba cạnh lần lượt bằng NGHỊCH ĐẢO độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Xét tam giác ABC như sau: ABC vuông tại A có AD là đường cao.
Ta có: \(AD=\dfrac{AB.AC}{BC}=\dfrac{4.3}{5}=2,4\)
Giả sử đề đúng thì có nghĩa là tồn tại tam giác vuông A'B'C' có độ dài 3 cạnh lần lược là: \(2,4;3;4\) sao cho tam giác này đồng đạng với tam giác ABC.
Mà ta có: \(2,4^2+3^2=14,76< 16=4^2\)
Theo Pitago thì A'B'C' không phải là tam giác vuông. Nên không thể đồng dạng với tam giác ABC được.
Vậy đề sai.
Giả sử tam giác có 3 cạnh lần lược là \(a,b,c\) và có 3 đường cao tương ứng là: \(h_a,h_b,h_c\)
Ta có: \(S_{ABC}=\dfrac{1}{2}.a.h_a=\dfrac{1}{2}.b.h_b=\dfrac{1}{2}.c.h_c\)
\(\Leftrightarrow a.h_a=b.h_b=c.h_c\)
\(\Leftrightarrow\dfrac{a}{\dfrac{1}{h_a}}=\dfrac{b}{\dfrac{1}{h_b}}=\dfrac{c}{\dfrac{1}{h_c}}\)
Vậy tam giác ABC có độ dài các cạnh là \(a,b,c\) sẽ đồng dạng với tam giác A'B'C' có độ dài các cạnh là: \(\dfrac{1}{h_a};\dfrac{1}{h_b};\dfrac{1}{h_c}\) (Điều phải chứng minh).
Giả sử tam giác có 3 cạnh lần lược là a,b,ca,b,c và có 3 đường cao tương ứng là: ha,hb,hcha,hb,hc
Ta có: SABC=12.a.ha=12.b.hb=12.c.hcSABC=12.a.ha=12.b.hb=12.c.hc
⇔a.ha=b.hb=c.hc⇔a.ha=b.hb=c.hc
⇔a1ha=b1hb=c1hc⇔a1ha=b1hb=c1hc
Vậy tam giác ABC có độ dài các cạnh là a,b,ca,b,c sẽ đồng dạng với tam giác A'B'C' có độ dài các cạnh là: 1ha;1hb;1hc1ha;1hb;1hc (Điều phải chứng minh).
Xét tam giác ABC như sau: ABC vuông tại A có AD là đường cao.
Ta có: AD=AB.ACBC=4.35=2,4AD=AB.ACBC=4.35=2,4
Giả sử đề đúng thì có nghĩa là tồn tại tam giác vuông A'B'C' có độ dài 3 cạnh lần lược là: 2,4;3;42,4;3;4 sao cho tam giác này đồng đạng với tam giác ABC.
Mà ta có: 2,42+32=14,76<16=422,42+32=14,76<16=42
Theo Pitago thì A'B'C' không phải là tam giác vuông. Nên không thể đồng dạng với tam giác ABC được.
Vậy đề sai.
a)∆ADB và ∆CDI , ta có :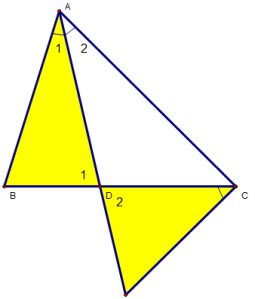
(gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) )∆ABD và ∆AIC , ta có :
(∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c)=> AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :
AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
1. AC2 = CH.BC :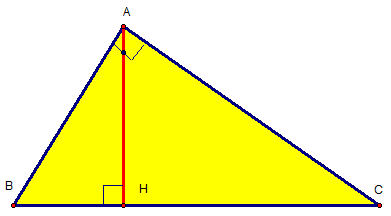
Xét hai ∆ABC và ∆ HAC, ta có :
là góc chung.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
2. AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
3.AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
=>
=> AH2 = BH.CH
4. AH.BC = AB.AC :
Ta có : (∆ABC ~ ∆HAC)
=> AH.BC = AB.AC.
a) xét ∆ABD và ∆AEG, ta có :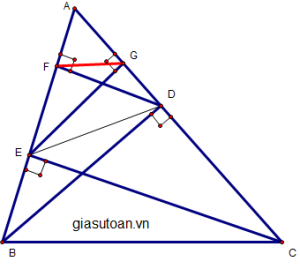
BD AC (BD là đường cao)
EG AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :
AB.AG = AC.AF (cmt)
=> FG // BC (định lí đảo talet)
a)xét ∆HBE và ∆HCD, ta có :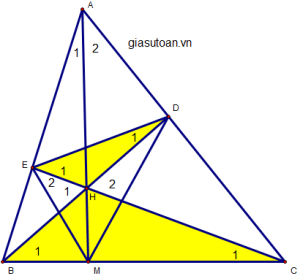
(gt)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, ta có :
(∆HBE ~ ∆HCD)
=>
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=> (1)
mà : đường cao BD và CE cắt nhau tại H (gt)
=> H là trực tâm.
=> AH BC tại M.
=>
mặt khác :
=> (2)
từ (1) và (2) :
hay :
c) cmtt câu b, ta được : (3)
xét ∆BCD, ta có :
DB = DC (gt)
=> ∆BCD cân tại D
=>
mà : (∆HED ~ ∆HBC)
=>
mà :
(cmt)
=>
hay :
=> ED EM.


















