
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra 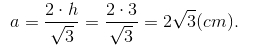 Do đó diện tích tam giác ABC là
Do đó diện tích tam giác ABC là
 Ta chọn (D).
Ta chọn (D).

Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra 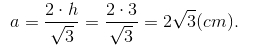 Do đó diện tích tam giác ABC là
Do đó diện tích tam giác ABC là
 Ta chọn (D).
Ta chọn (D).
Cho tam giác ABC vuông ở A R,r : Bán kính của đường kính ngoại tiếp ,nội tiếp tam giác ABC CMR: câu a r=1/2(AB+AC-BC) câu b AB+AC=2(R+r)
Độ dài mỗi cạnh của tam giác đều ngoại tiếp đường tròn (O; r) bằng :
(A) \(r\sqrt{3}\) (B) \(2r\sqrt{3}\) (C) \(4r\) (D) \(2r\)
Hãy chọn phương án đúng ?
Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp, r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng :
\(AB+AC=2\left(R+r\right)\)
Cho tam giác ABC vuông ở A R,r : Bán kính của đường kính ngoại tiếp ,nội tiếp tam giác ABC CMR: câu a r=1/2(AB+AC-BC) câu b AB+AC=2(R+r)
Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I; r) ?
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D, E
a) Tứ giác ADOE là hình gì ? Vì sao ?
b) Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm ?
3) Cho đường tròn tâm O, bán kính R. Lấy điểm A cách O một khoảng = 2R. Từ A vẽ 2 tiếp tuyến AB, AC (B,C là tiếp điểm).
a. CM : AOB là nửa tam giác đều
b. Tính các cạnh của tam giác ABC
c. :Đường thẳng qua O và vuông góc với OB cắt AC tại K. CM ; AKO cân
d: gọi I là trung điểm của đoạn thẳng OA . CM đường thẳng BC cắt tiếp tuyến của (O) . tính IK theo R
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức :
\(S=p.r\)
Cho tam giác ABC có AB = 5cm, AC = 7cm, BC = 6cm ngoại tiếp đường tròn (O). Đường tròn (O1) bằng tiếp góc A tiếp xúc với cạnh BC ở D, tiếp xúc với phần kéo dài của các cạnh AB, AC lần lượt ở E và F.
a) Chứng minh ba điểm A, O, O1, thẳng hàng
b) Tính độ dài các đoạn AE, AF. BE, CF