Question

Cho tam giác ABC vuông tại A,đường cao AH biết AB = 3cm, BH = 1,8cm. Tính V, S_xq hình tạo thành khi quay tam giác vuông ABC quanh trục AB

Answer 1

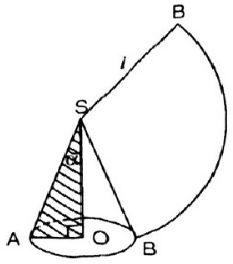
Lời giải:

Theo công thức hệ thức lượng trong tam giác vuông ta có:

\(AB^2=BH.BC\Leftrightarrow 9=1,8.BC\Rightarrow BC=5\) (cm)

Định lý Pitago: \(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\) (cm)

Như vậy, khi quay tam giác $ABC$ quanh trục $AB$ ta thu được hình nón có đường cao \(AB=3\), bán kính đáy \(AC=4\) và đường sinh \(BC=5\)

Diện tích xung quanh của hình nón thu được:

\(S_{\text{xq}}=\pi rl=\pi. AC.BC=20\pi \) (cm vuông)

Thể tích hình nón là:

\(V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi. 4^2.3=16\pi \) (cm khối)