Chương II : Tam giác
Các câu hỏi tương tự
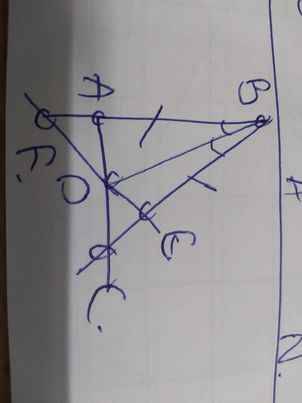
Cho tam giác ABC vuông tại A. Kẻ BD là phân giác của ABC (D ϵ AC). Trên đoạn BC lấy điểm E sao cho AB = BE
a, Chứng minh AD = DE
b, Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh BD vuông FC
c, Chứng minh AF // FC
d, Chứng minh ba điểm D, E, F thẳng hàng
Cho tam giác ABC vuông tại A. Kẻ BD là phân giác của ABC (D ϵ AC). Trên đoạn BC lấy điểm E sao cho AB = BE
a, Chứng minh AD = DE
b, Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh BD vuông FC
c, Chứng minh AE // FC
d, Chứng minh ba điểm D, E, F thẳng hàng
Cho tam giác ABC vuông tại A có phân giác BD ( D thuộc AC). Trên cạnh BC lấy điểm E sao cho AE = BE. Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Gọi I là giao điểm của BD và FC. Chứng minh rằng:
a) Tam giác ABD = Tam giác EBD
b) DE vuông góc với BC
c) BD là trung trực của đoạn thẳng AE
d) Ba điểm D , E , F thẳng hàng
e) Điểm D cách đều ba cạnh của tam giác AEI
Cho tam giác ABC vuông tại A, trung điểm M của cạnh BC. Trên tia đối của
tia MA, lấy điểm D sao cho MA = MD.
a) Chứng minh tam giác MAB= tam giác MDC.
b) Chứng minh AB//CD.
c) Lấy E là trung điểm AC, kẻ MF vuông góc BD , chứng ming ba điểm E, M, F thẳng hàng.
Cho tam giác ABC vuông tại A. Đường phân giác BD. Vẽ DE vuông góc với BC (E thuộc BC)a) Chứng minh: BAD BEDb) DA DCc) Trên tia đối của tia AB lấy điểm F sao cho AF EC. Chứng minh DFC când) Chung minh ba điểm F, D, E thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường phân giác BD. Vẽ DE vuông góc với BC (E thuộc BC)
a) Chứng minh: BAD = BED
b) DA < DC
c) Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh DFC cân
d) Chung minh ba điểm F, D, E thẳng hàng.
cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BEBA. Trên tia BA lấy điểm F sao cho BFBC. Kẻ BD là tia phân giác của góc ABC(D thuộc AC). Chứng minh rằng:a) Tam giác ABD tam giác EBD từ đó suy ra AD EDb) BD là đg trung trực của đoạn thẳng AE và AD DCc) Ba điểm E ,D, F thẳng hàng
Đọc tiếp
cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Trên tia BA lấy điểm F sao cho BF=BC. Kẻ BD là tia phân giác của góc ABC(D thuộc AC). Chứng minh rằng:
a) Tam giác ABD = tam giác EBD từ đó suy ra AD = ED
b) BD là đg trung trực của đoạn thẳng AE và AD < DC
c) Ba điểm E ,D, F thẳng hàng
Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC
a) Chứng minh: △AHB = △AHC và AH vuông góc với BC.
b) Kẻ HE ⊥ AB(E ϵ AB), HF ⊥ AC(F ϵ AC). Chứng minh △HEB = △HFC.
c) Trên tia đối của tia HA lấy điểm D sao cho H là trung điểm của AD. Chứng minh rằng FH ⊥ BD
Cho tam giác ABC vuông tại A, trên cạnh BC lấy điểm D sao cho BD=AB. Qua D kẻ đường thẳng vuông góc với BC, cắt cạnh AC tại E.
a) Chứng minh: tam giác BAE = tam giác BDE. Suy ra: AE = ED.
b) Gọi F là giao điểm của tia DE và tia BA. Chứng minh: tam giác FEC cân.
c) Gọi K là trung điểm của FC. Chứng minh: B, E, K thẳng hàng.
Giúp mình vs!!!!!
Cho △ABC có AB < AC, phân giác AD (D∈BC). Trên tia AC lấy điểm E sao cho AE = AB.
a) Chứng minh rằng BD = DE
b) Gọi K là giao điểm của các đường thẳng AB và ED. Chứng minh rằng △DBK = △DEC
c) △AKC là tam giác gì ? Chứng minh
d) Chứng minh AD ⊥ KC