Question

Cho tam giác ABC vuông tại A có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm N sao cho MN=MA. a) Chứng minh: AB = NC , tam giác CAN vuông b) Chứng minh: AM = 1/2 BC c) Kẻ MK vuông góc với BN , MI vuông góc với AC . CM I, M , K Thẳng hàng

Answer 1

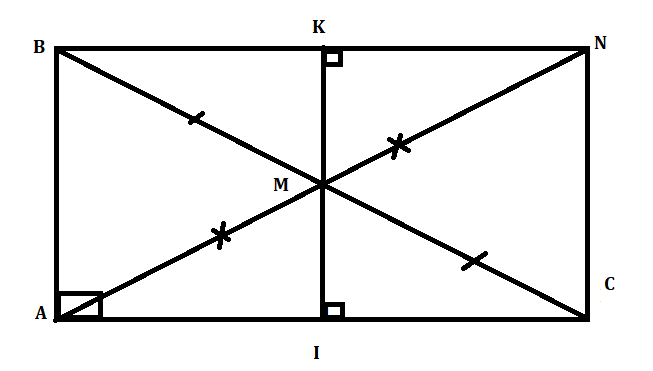
a: Xét tứ giác ABNC có 

M là trung điểm của BC

M là trung điểm của AN

Do đó: ABNC là hình bình hành

mà \(\widehat{CAB}=90^0\)

nên ABNC là hình chữ nhật

Suy ra: AB=NC và ΔCAN vuông tại C

b: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên AM=1/2BC

Answer 2

a) Xét tam giác MAB và tam giác MCN có 
MB =MC ( M là tđ BC)

AM =AN (gt)

AMB = CMD ( 2 góc đối đỉnh ) 

=> 2 tam giác = nhau (c-g-c) 

=> AB =NC (2 cạnh tương ứng)

=> góc BAN = góc ANC (2 góc tương ứng)

mà 2 góc ở vị trí so le trong => AB // NC 

=> A + C = 180 ( 2 góc trong cùng phía bù nhau) 

=> 90 + c = 180 => góc C=90 

xét tam giác ACN có góc C =90 => tma giác ACN vuông tại C

b) Xét tam giác ABC vuông tại A có M là trung điểm BC => AM là trung tuyến => AM = BM = CM =1/2 BC(tc) 

c) ta xét tam giác BAN có : AM =MN => M là trung điểm của AN => BM là trung tuyến của AN 

mà BM = AM (cmt ) => BM=AM=MN=1/2AN 

=> tam giác ABN vuông tại B => AB vuông góc với BN 

mà MK vuông góc với BN (gt)=> AB // MK ( từ vuông góc -> //)

mà AB vuông góc AC => MK vuông góc với AC (từ vuông góc -> //)

ta lại có MI cũng vuông góc với AC (gt)

=> M,K,I thẳng hàng (tiên đề ơ clits)

Answer 3