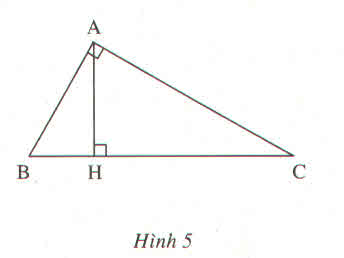
xét △ABH vuông tại H, có:
⇒ BH2 + AH2 =AB2 (py-ta-go)
⇒\((\frac{25}{13})^2+(\frac{60}{13})^2=AB^2\)
⇒\(\frac{625}{169}+\frac{3600}{169}=AB^2\)
⇒AB2 =25
⇒\(\sqrt{AB}=\sqrt{25}\)
⇒AB = 5 cm
Xét △ABC vuông tại A, AH là đường cao:
⇒\(AB^2=BH.BC\) (hệ thức lượng)
⇒AB2 =\(\frac{25}{13}.5\)
⇒AB2 = \(\frac{125}{13}\)
⇒AB =\(\frac{5\sqrt{65}}{13}cm\)
Xét △ABC vuông tại A, có:
⇒ AB2 +AC2 =BC2 (py-ta-go)
⇒ \((\frac{5\sqrt{65}}{13})^2+AC^2=5^2\)
⇒ \(\frac{125}{13}+AC^2=25\)
⇒AC2 = \(25-\frac{125}{13}\)
⇒AC =\(\frac{10\sqrt{26}}{13}cm\)