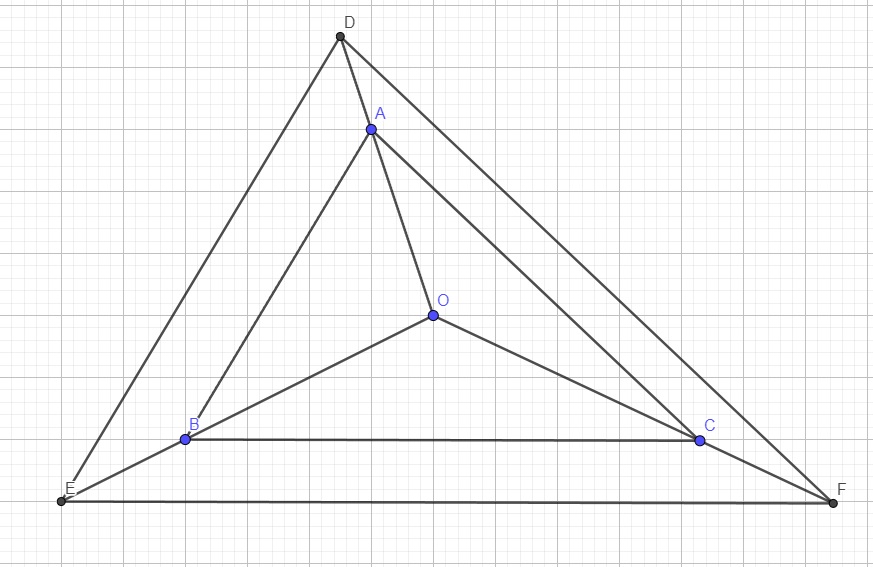
a.
Do AB song song DE, áp dụng định lý Talet:
\(\dfrac{AB}{DE}=\dfrac{OA}{OD}=\dfrac{2}{3}=\dfrac{OB}{OE}\) (1)
Do AC song song DF, áp dụng định lý Talet:
\(\dfrac{AC}{DF}=\dfrac{OA}{OD}=\dfrac{2}{3}=\dfrac{OC}{OF}\) (2)
(1);(2) \(\Rightarrow\dfrac{OB}{OE}=\dfrac{OC}{OF}\Rightarrow BC||EF\) (Talet đảo)
\(\Rightarrow\dfrac{BC}{EF}=\dfrac{OB}{OE}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}\Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)
b.
Ta có: \(\left\{{}\begin{matrix}\dfrac{AB}{DE}=\dfrac{2}{3}\\DE-AB=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{2}{3}DE\\DE-\dfrac{2}{3}DE=12\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}DE=36\\AB=\dfrac{2}{3}.36=24\end{matrix}\right.\)
c.
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{2}{3}=\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}=\dfrac{AB+AC+BC}{DE+DF+EF}\)
\(\Rightarrow AB+AC+BC=\dfrac{2}{3}\left(DE+DF+EF\right)\)
Mà \(\left(DE+DF+EF\right)+\left(AB+AC+BC\right)=120\)
\(\Rightarrow\left(DE+DF+EF\right)+\dfrac{2}{3}\left(DE+DF+EF\right)=120\)
\(\Rightarrow\dfrac{5}{3}\left(DE+DF+EF\right)=120\)
\(\Rightarrow DE+DF+EF=72\)