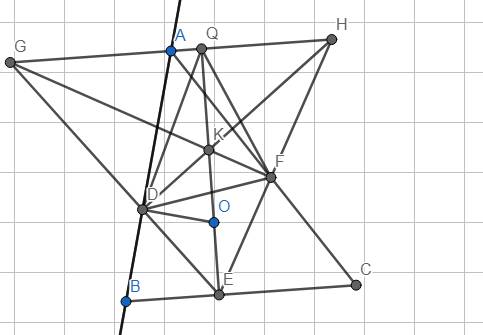
1) Vì \(\left(O\right)\) nội tiếp △ABC và tiếp xúc với AB,BC,CA lần lượt tại D,E,F.
\(\Rightarrow\left\{{}\begin{matrix}BE=BD\\AD=AF\\CE=CF\end{matrix}\right.\) và \(\left\{{}\begin{matrix}OD\perp ABtạiD\\OE\perp BCtạiE\\OF\perp CAtạiF\end{matrix}\right.\)
\(BD+BE=AB-AD+BC-CE=AB+BC-AF-CF=AB+BC-CA\)
\(\Rightarrow2BD=c+a-b\)
\(\Rightarrow BD=\dfrac{c+a-b}{2}\)
\(\Rightarrow AD=AB-BD=c-\dfrac{c+a-b}{2}=\dfrac{c+b-a}{2}\)
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{\dfrac{c+b-a}{2}}{\dfrac{c+a-b}{2}}=\dfrac{c+b-a}{c+a-b}\)
Xét △BDE có: BE//AG.
\(\Rightarrow\dfrac{DG}{DE}=\dfrac{AD}{BD}=\dfrac{c+b-a}{c+a-b}\) (định lí Ta-let).
2) \(BD=BE\Rightarrow\)△BDE cân tại B.
\(\Rightarrow\widehat{BDE}=\widehat{BED}\) mà \(\left\{{}\begin{matrix}\widehat{BDE}=\widehat{ADG}\\\widehat{BED}=\widehat{AGD}\end{matrix}\right.\)
\(\Rightarrow\widehat{ADG}=\widehat{AGD}\Rightarrow\)△ADG cân tại A.
\(\Rightarrow AD=AG=AF\)
Tương tự \(AH=AF\Rightarrow AG=AH\)
\(\Rightarrow\)A là trung điểm GH.
\(\Rightarrow DA=DF=AG=\dfrac{1}{2}GH\)
△DHG có: DA là trung tuyến và \(DA=\dfrac{1}{2}GH\)
\(\Rightarrow\)△DHG vuông tại D.
\(\Rightarrow\)HD là đường cao của △GHE (1).
Tương tự: GF là đường cao của △GHE (2).
Ta có \(OE\perp BC\) mà BC//GH \(\Rightarrow OE\perp GH\)
\(\Rightarrow\)OE là đường cao của △GHE (3).
(1),(2),(3) \(\Rightarrow\)GF, HD, OE đồng quy.
3) \(EO\perp GH\) tại Q.
Gọi K là trực tâm của △GHE.
Vì △KDE, △KFE nội tiếp đường tròn đường kính KE nên:
K,D,E,F cùng thuộc 1 đường tròn.
Mà \(D,E,F\in\left(O\right)\Rightarrow K\in\left(O\right)\).
Chứng minh K là tâm đường tròn nội tiếp △DFQ \(\Rightarrow\)Sử dụng tam giác đồng dạng và tính chất 3 đg cao trong △DFQ.