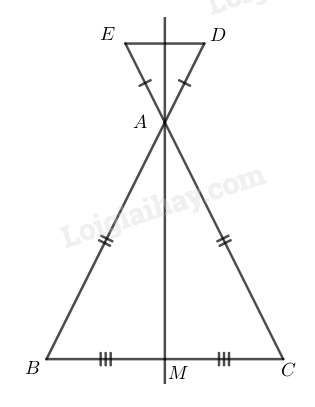
Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\) có:
\(AM\) là đường trung tuyến (vì \(M\) là trung điểm của \(BC\))
=> \(AM\) đồng thời là đường phân giác của \(\widehat{BAC}.\)
=> \(\widehat{BAM}=\widehat{MAC}\) (1)
Kéo dài \(AM\) cắt \(DE\) tại N, ta có:
\(\left\{{}\begin{matrix}\widehat{BAM}=\widehat{DAN}\left(2\right)\\\widehat{MAC}=\widehat{NAE}\left(3\right)\end{matrix}\right.\) (vì 2 góc đối đỉnh)
Từ \(\left(1\right),\left(2\right)và\left(3\right)\Rightarrow\widehat{DAN}=\widehat{NAE}.\)
Xét \(\Delta ADE\) có: \(AD=AE\left(gt\right)\)
=> \(\Delta ADE\) cân tại A.
Có \(AN\) là tia phân giác (do cách vẽ).
=> \(AN\) đồng thời là đường trung trực của \(DE.\)
Hay \(AM\) là đường trung trực của \(DE.\)
=> \(D\) đối xứng với \(E\) qua \(AM\left(đpcm\right).\)
Chúc bạn học tốt!










