Đề thiếu nha bạn
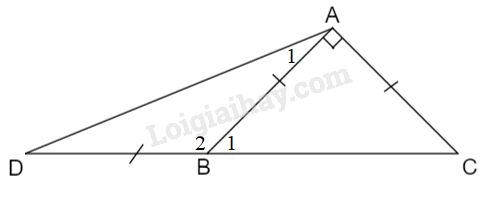
Sửa đề là \(\Delta ABC\) vuông cân tại \(A\) nhé.
+ Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)
=> \(\widehat{B_1}=\widehat{C}\) (tính chất tam giác cân).
+ Vì \(\Delta ABC\) vuông tại \(A\left(gt\right)\)
=> \(\widehat{B_1}+\widehat{C}=90^0\) (tính chất tam giác vuông).
Mà \(\widehat{B_1}=\widehat{C}\left(cmt\right)\)
=> \(\widehat{B_1}=\widehat{C}=\frac{90^0}{2}=45^0.\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\) (vì 2 góc kề bù).
=> \(45^0+\widehat{B_2}=180^0\)
=> \(\widehat{B_2}=180^0-45^0\)
=> \(\widehat{B_2}=135^0.\)
+ Xét \(\Delta ABD\) có:
\(BD=BA\left(gt\right)\)
=> \(\Delta ABD\) cân tại \(B.\)
=> \(\widehat{ADB}=\widehat{A_1}\) (tính chất tam giác cân).
+ Xét \(\Delta ABD\) có:
\(\widehat{A_1}+\widehat{B_2}+\widehat{ADB}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{ADB}+\widehat{B_2}+\widehat{ADB}=180^0\)
=> \(2\widehat{ADB}+\widehat{B_2}=180^0\)
=> \(2\widehat{ADB}+135^0=180^0\)
=> \(2\widehat{ADB}=180^0-135^0\)
=> \(2\widehat{ADB}=45^0\)
=> \(\widehat{ADB}=45^0:2\)
=> \(\widehat{ADB}=22,5^0.\)
Vậy \(\widehat{ADB}=22,5^0.\)
Chúc bạn học tốt!
ΔABC cân chứ có vuông tại A ko bạn
Sửa đề: Cho tam giác ABC vuông cân tại A.
Vì tam giác ABC vuông cân tại A => góc B = góc C = 45 độ
Ta có: góc ABC + góc ABD = 180 độ ( 2 góc kề bù )
Mà góc ABC = 45 độ ( cmt )
=> góc ABD = 180 độ - 45 độ = 135 độ
Xét tam giác BAD có:
BA=BD ( gt )
=> Tam giác BAD cân tại B
=> góc BAD = góc BDA = \(\frac{180^o-\widehat{DBA}}{2}=\frac{180^o-135^o}{2}=22,5^o\)( do mình lấy gần bằng nhé )
P/s: Xin lỗi vì mình không biết vẽ hình!
Ta có: tam giác ABC vuông cân tại A
=> góc ABC = \(45^o\)
Ta có: góc ABC + góc ABD = \(180^o\)
hay \(45^o\) + góc ABD = \(180^o\)
=> góc ABD = \(180^o\) - \(45^o\) = \(135^o\)
Ta có: góc DAB + góc ABD + góc ADB = \(180^o\)
hay góc DAB + góc ADB + \(135^o\) = \(180^o\)
=> góc DAB + góc ADB = \(45^o\)
Ta có: BD = BA => tam giác BDA cân
=> góc DAB = góc ADB = \(45^o\)/2 = \(22,5^o\)
















