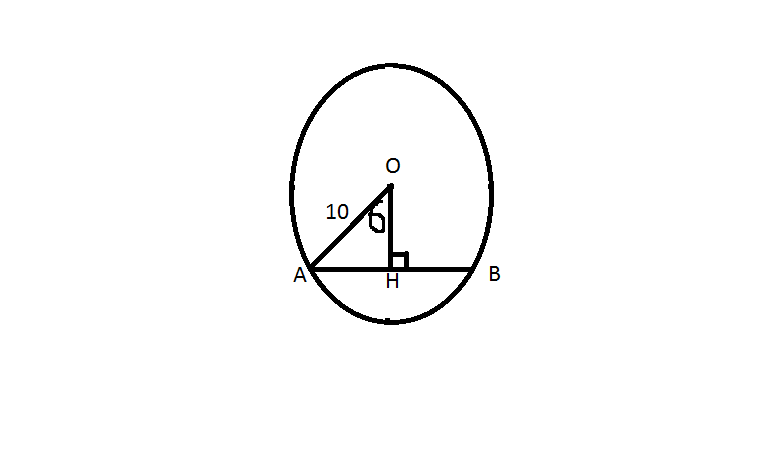
Từ O kẻ OH\(\perp\)AB.
Có OA=OB\(\Rightarrow\Delta OAB\) cân tại O.
Suy ra H là trung điểm AB( tính chất tam giác cân)
Xét tam giác OAH vuông tại H:
\(AH=\sqrt{OA^2-OH^2}=\sqrt{10^2-6^2}=8\)cm
\(\Rightarrow AB=2AH=2\cdot8=16cm\)
Cho đường tròn (O;5cm) và dây cung AB =6 cm. Gọi E là trung điểm của AB, OE cắt (O) tại M. Độ dài dây AM là:
Cho đường tròn (O) và một dây cung AB. Gọi H là trung điểm của đoạn thẳng Ab, biết OH=6cm;AB=16cm. Bán kính của đường tròn (O) bằng
A.5cm
B.\(12\sqrt{2}\) cm
C.\(2\sqrt{7}\) cm
D.10cm
Cho (O;13cm), M là trung điểm của dây AB sao cho OM = 5cm. Độ dài dây AB là
Cho tia Ax là tia tiếp tuyến của (O) (A thuộc (O)). Vẽ dây AB sao cho xAB 60 . Số đo cung lớn AB bằng
AB và CD là hai dây cung của đường tròn (O) cố định .Trong đó dây AB cố định, dây CD di động trên cung lớn AB sao cho BC song song với AD . Gọi M là giao điểm của AC và BD
a) tứ giác ABCDlà hình j ?
b) CM 4 điểm A,M,O,B thuộc 1 đường tròn .
c) CM OM⊥BC
Cho (O;R), dây cung BC( khác đg kính). Điểm A di động trên cung lớn BC(A khác B,C). Kẻ đg kính AD của (O), H là chân đg vuông góc kẻ từ A đến BC. Hai đ E,F lần lượt là chân đuong vuông góc kẻ từ B,C đến AD.CMR:
1.A,B,H,E cùng thuộc 1 đường tròn
2.R=(AB.AC):(2AH)
3.HE vuông góc AC và tâm đg tròn ngoại tiếp tam giác HEF là 1 điểm cố định
Cho đường tròn tâm O, đường kính AB=2R, điểm C thuộc đường tròn O mà góc ABC bằng 30 độ, vẽ dây CD vuông góc với AB tại H, gọi M là điểm chính giữa của cung BC, I là giao điểm của BC và OM. a) chứng minh HCIO nội tiếp b) Gọi K là giao điểm của AM và BC. Chứng minh KC=2KB
Từ điểm A ngoài đường tròn O,R về. 2 tiếp tuyến AB, AC các tuyến AMN của đường tròn, i là trung điểm dây MN
Cm 5 điểm A,B I O C nằm trên 1 đng tròn
Cm AB ^2 = AC ^2 = AM .AN
Cho AB=R√3 tính diện tích viên phân giới hạn dây BC và cung BC theo R
