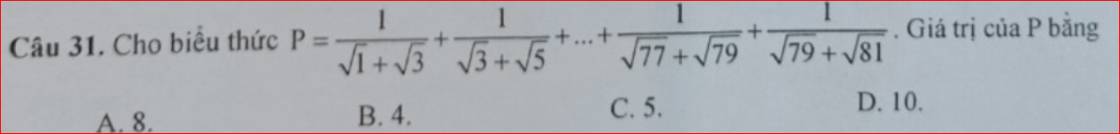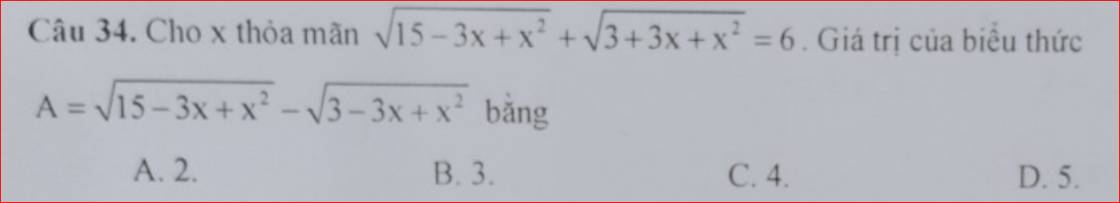\(P=\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{77}+\sqrt{79}}+\dfrac{1}{\sqrt{79}+\sqrt{81}}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}}{\left(\sqrt{1}+\sqrt{3}\right)\left(\sqrt{1}-\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{5}}{\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{3}-\sqrt{5}\right)}+...+\dfrac{\sqrt{79}-\sqrt{81}}{\left(\sqrt{79}+\sqrt{81}\right)\left(\sqrt{79}-\sqrt{81}\right)}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}}{1-3}+\dfrac{\sqrt{3}-\sqrt{5}}{3-5}+...+\dfrac{\sqrt{79}-\sqrt{81}}{79-81}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}+\sqrt{3}-\sqrt{5}+\sqrt{5}-\sqrt{7}+...+\sqrt{77}-\sqrt{79}+\sqrt{79}-\sqrt{81}}{-2}\)
\(P=\dfrac{1-9}{-2}\)
\(P=\dfrac{-8}{-2}\)
\(P=4\)
⇒ Chọn B
\(P=\dfrac{\sqrt{3}-1}{2}+\dfrac{\sqrt{5}-\sqrt{3}}{2}+...+\dfrac{\sqrt{81}-\sqrt{79}}{2}\)
\(=\dfrac{-1+\sqrt{3}-\sqrt{3}+\sqrt{5}-...-\sqrt{79}+9}{2}=\dfrac{8}{2}=4\)