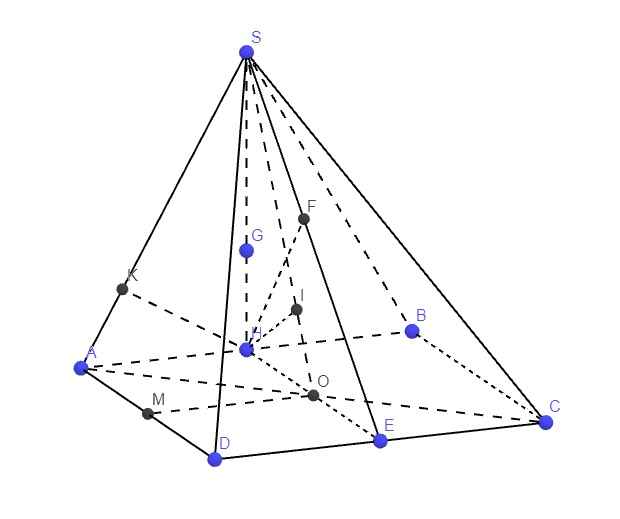
a.
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)
d.
Gọi M là trung điểm AD \(\Rightarrow OM||CD\Rightarrow CD||\left(SOM\right)\)
\(\Rightarrow d\left(CD;SO\right)=d\left(CD;\left(SOM\right)\right)=d\left(E;\left(SOM\right)\right)\)
Mà \(\left\{{}\begin{matrix}HE\cap\left(SOM\right)=O\\HO=EO\end{matrix}\right.\)
\(\Rightarrow d\left(E;\left(SOM\right)\right)=d\left(H;\left(SOM\right)\right)\)
Từ H kẻ \(HI\perp SO\)
\(OM||CD\Rightarrow OM\perp\left(SHE\right)\Rightarrow OM\perp HI\)
\(\Rightarrow HI\perp\left(SOM\right)\Rightarrow HI=d\left(H;\left(SOM\right)\right)\)
\(OH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Hệ thức lượng:
\(HI=\dfrac{SH.HO}{\sqrt{SH^2+HO^2}}=\dfrac{a\sqrt{3}}{4}\)