Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
bài 1 Cho hình thang ABCD có AB//CD và CDAB . Gọi O là giao điểm của AC và BD cắt đương thẳng kẻ từ A và B lần lượt song song vơi BC và AD , cắt các đường chéo BD và AC tương ứng với F và E
a, EF//AB
b, AB2 EF.CD
Bài 2 Cho góc nhọn xoy trên cạnh ox lấy M , trên cạnh oy lấy N . GỌi A là điểm nằm trên đoạn MN , qua A kẻ đường thẳng song song ox cắt oy ở Q với đường thẳng song song với oy cắt ox ở P . CMr
OB/OM + OQ/ON1
Giúp mình với tối mai đi hc rồi
Đọc tiếp
bài 1 Cho hình thang ABCD có AB//CD và CD>AB . Gọi O là giao điểm của AC và BD cắt đương thẳng kẻ từ A và B lần lượt song song vơi BC và AD , cắt các đường chéo BD và AC tương ứng với F và E
a, EF//AB
b, AB2= EF.CD
Bài 2 Cho góc nhọn xoy trên cạnh ox lấy M , trên cạnh oy lấy N . GỌi A là điểm nằm trên đoạn MN , qua A kẻ đường thẳng song song ox cắt oy ở Q với đường thẳng song song với oy cắt ox ở P . CMr
OB/OM + OQ/ON=1
Giúp mình với tối mai đi hc rồi
Cho tam giác AOB có AB = 18cm, OA = 12cm, OB = 9cm. Trên tia đối của tia OB lấy điểm D sao cho OD = 3cm. Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC. Tính tỉ số \(\dfrac{FD}{FA}\)
1. Cho widehat{xAyne} góc bẹt. Trên Ax lấy hai điểm B và D, trên Ay lấy hai điểm C và E. Sao cho frac{AD}{BD}frac{11}{8} và ACfrac{3}{8}CE
a) Chứng minh: BC//DE
b) Biết BC3cm. Tính DE
2. Cho hình thang ABCD (AB//CD) có AB7,5cm, CD12cm . Gọi M là trung điểm của CD, E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh: EF//AB
b) Tính độ dài đoạn EF
3. Cho widehat{xOy} nhọn. Trên cạnh Ox lấy điểm M, trên cạnh Oy lấy điểm N. Gọi A là 1 điểm trên cạnh MN, qua A kẻ đường thẳ...
Đọc tiếp
1. Cho \(\widehat{xAy\ne}\) góc bẹt. Trên Ax lấy hai điểm B và D, trên Ay lấy hai điểm C và E. Sao cho \(\frac{AD}{BD}=\frac{11}{8}\) và \(AC=\frac{3}{8}CE\)
a) Chứng minh: BC//DE
b) Biết \(BC=3cm\). Tính DE
2. Cho hình thang ABCD (AB//CD) có \(AB=7,5cm\), \(CD=12cm\) . Gọi M là trung điểm của CD, E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh: EF//AB
b) Tính độ dài đoạn EF
3. Cho \(\widehat{xOy}\) nhọn. Trên cạnh Ox lấy điểm M, trên cạnh Oy lấy điểm N. Gọi A là 1 điểm trên cạnh MN, qua A kẻ đường thẳng // với Ox cắt Oy ở Q, và đường thẳng // Oy cắt Ox ở P
Chứng minh: \(\frac{OP}{OM}+\frac{OQ}{ON}=1\)
*Lưu ý: Có vẽ hình và khi chứng minh cần có dấu hiệu trong( ... ). Vd: tam giác ABC cân ⇒ AB=AC (tính chất tam giác cân)
Thần đồng toán học:
Nguyễn Thành Trương, Băng Băng 2k6 Nguyễn Văn Đạt Akai Haruma Trần Thanh Phương tth
Cho tam giác ABC có O nằm trong tam giác. Đường thẳng qua O song song với BC cắt AB,AC tại M,N. Đường thẳng qua O song song với AB cắt AC, BC tại F, E. Đường thẳng qua O song song với AC cắt AB, BC tại I, K.
Chứng minh: \(\dfrac{AI}{AB}+\dfrac{BE}{BC}+\dfrac{CN}{AC}=1\)
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho dfrac{AE}{ED}dfrac{p}{q}. Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
Chứng minh rằng :
EFdfrac{p.CD+q.AB}{p+q}
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Đọc tiếp
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho \(\dfrac{AE}{ED}=\dfrac{p}{q}\). Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
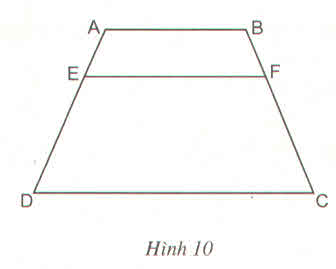
Chứng minh rằng :
\(EF=\dfrac{p.CD+q.AB}{p+q}\)
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Cho hình thang ABCD (AB // CD) có O là giao điểm của hai đường chéo AC và BD. Qua A, kẻ đường thẳng song song với BC cắt BD tại E. Qua B, kẻ đường thẳng song song với AD cắt AC tại F.
a) Chứng minh: EF // CD.
b) Chứng minh: AB2 = CD . EF
Cho tam giác ABC có AB = 18 cm, AC = 12 cm, BC = 9 cm. Trên tia đối của tia CB lấy điểm D sao cho CD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AC tại E. Gọi F là giao điểm của AD và BE. Tính: a) Độ dài CE, DE
Cho tứ giác ABCD. Qua E thuộc cạnh AD, kẻ đường thẳng song song với DC cắt AC tại G. Qua G kẻ đường thẳng song song CB cắt AB tại H. a. Chứng minh: HE song song BD. b. Qua B kẻ đường thẳng song song với CD cắt AC tại I. Qua C kẻ đường thẳng song song với BA cắt BA tại F. Chứng minh: IF song song AD.













