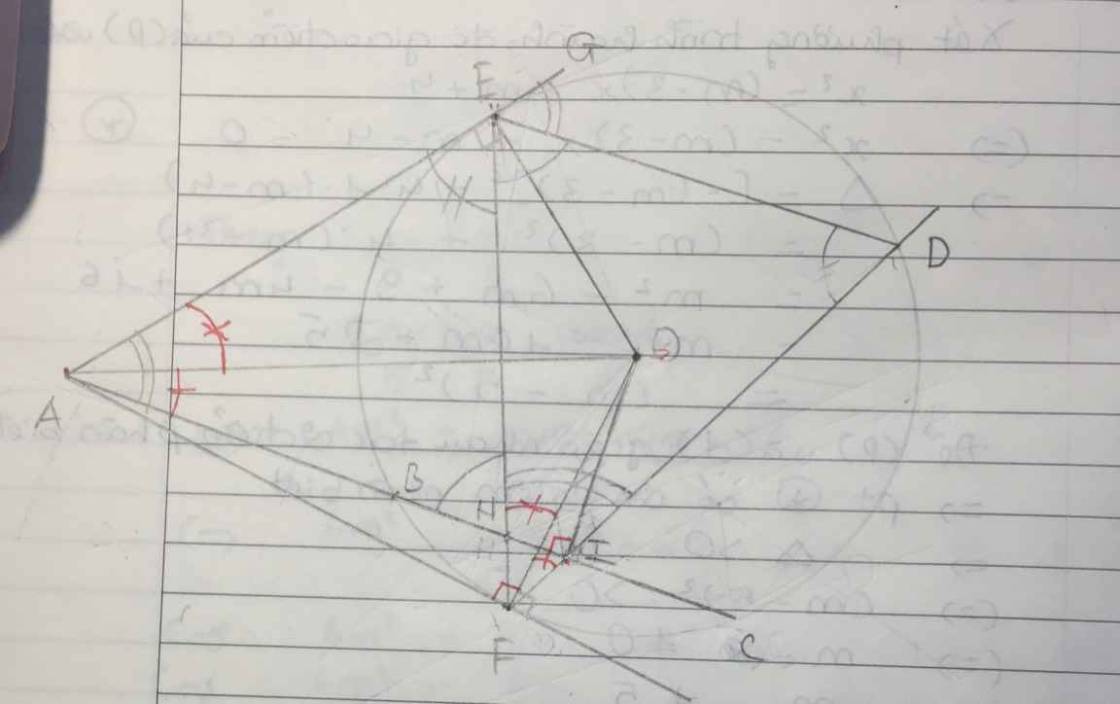
Cho đường tròn (O;R) có đường kính BC. Trên tia đối của tia BC lấy cung DE của đường tròn (O) vuông góc với BC
a) AE là tiếp tuyến của đường tròn (O)
b) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao điểm của 2 đường thẳng BD và AE. Chứng minh BC//EF và PO.GE=PC.GB
c) Vẽ cát tuyến AMN của đường tròn (O) ( cát tuyến không đi qua O ), các tuyến tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K,D,E thẳng hàng.
Sửa đề: Trên tia đối của tia BC lấy E, kẻ AD là tiếp tuyến tại D của (O) và vẽ DE⊥BC(E∈(O))
a: ΔODE cân tại O
mà OA là đường cao
nên OA là phân giác của góc DOE
Xét ΔODA và ΔOEA có
OD=OE
\(\hat{DOA}=\hat{EOA}\)
OA chung
Do đó: ΔODA=ΔOEA
=>\(\hat{ODA}=\hat{OEA}\)
=>\(\hat{OEA}=90^0\)
=>AE là tiếp tuyến tại E của (O)
b: Xét (O) có
ΔDEF nội tiếp
DF là đường kính
Do đó: ΔDEF vuông tại E
=>DE⊥EF
mà DE⊥BC
nên BC//EF
c: Gọi H là giao điểm của DE và OA
Kẻ OI⊥MN tại I, gọi X là giao điểm của OI và DE
Xét ΔOIA vuông tại I và ΔOHX vuông tại H có
\(\hat{IOA}\) chung
Do đó: ΔOIA~ΔOHX
=>\(\frac{OI}{OH}=\frac{OA}{OX}\)
=>\(OH\cdot OA=OI\cdot OX\)
Xét ΔODA vuông tại D có DH là đường cao
nên \(OH\cdot OA=OD^2\)
=>\(OI\cdot OX=OD^2=R^2\)
=>\(OI\cdot OX=ON^2\)
=>\(\frac{OI}{ON}=\frac{ON}{OX}\)
Xét ΔOIN và ΔONX có
\(\frac{OI}{ON}=\frac{ON}{OX}\)
góc ION chung
DO đó: ΔOIN~ΔONX
=>\(\hat{OIN}=\hat{ONX}\)
=>\(\hat{ONX}=90^0\)
=>XN là tiếp tuyến tại N của (O)
Xét (O) có
KM,KN là các tiếp tuyến
Do đó: KM=KN
=>K nằm trên đường trung trực của MN(1)
ΔOMN cân tại O
mà OI là đường cao
nên OI là đường trung trực của MN(2)
Từ (1),(2) suy ra O,I,K thẳng hàng
mà O,I,X thẳng hàng
và XN và KN đều là tiếp tuyến tại N của (O)
nên K trùng với X
=>K,D,E thẳng hàng