Question

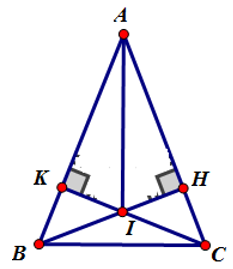
Cho ΔABC cân tại A (góc A<90^o). Vẽ BH⊥AC (H ∈ AC), CK⊥AB (K ∈ AB).

a) Chứng minh rằng AH = AK.

b)Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A.

GIÚP MÌNH VỚI!! MÌNH CẦN GẤP!!!

P/S: Cho mình hỏi cách để cài biểu tượng góc nha~~ Nó giống thế này (^) nhưng ở trên tên góc ấy...

P/S2: Mình vội quá chưa kịp vẽ hình. Các bạn tự vẽ nha~~~

Answer 1

a,Xét ΔABH vuông tại H và ΔACK vuông tại K có:

AB = AC (Do ΔABC cân tại A)

góc A chung

Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).

b, Xét ΔKBC,ΔHCB có :

KBCˆ=HCBˆ(​Tam giác ABC cân tại A)

BC:Chung

BKCˆ=CHBˆ(=90^o)

=> ΔKBC=ΔHCB (cạnh huyền - góc nhọn)

=> KCBˆ=HBCˆ(​2 góc tương ứng)

Xét ΔBIC có:

IBCˆ=ICBˆ (do KCBˆ=HBC- cmt)

=> ΔBIC cân tại I (đpcm)

Xét ΔABI,ΔACI có :

AB=AC(Δ​ABC cân tại A)

AI:Chung

BI=CI (ΔBIC cân tại I)

=> ΔABI=ΔACI(c.c.c)

=> BAIˆ=CAI (2 góc tương ứng)

Do đó : AI là tia phân giác của Aˆ

Answer 2

a) Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)

=> \(AB=AC\) (tính chất tam giác cân).

Xét 2 \(\Delta\) vuông \(ABH\) và \(ACK\) có:

\(\widehat{AHB}=\widehat{AKC}=90^0\left(gt\right)\)

\(AB=AC\left(cmt\right)\)

\(\widehat{A}\) chung

=> \(\Delta ABH=\Delta ACK\) (cạnh huyền - góc nhọn).

=> \(AH=AK\) (2 cạnh tương ứng).

b) Theo câu a) ta có \(\Delta ABH=\Delta ACK.\)

=> \(\widehat{ABH}=\widehat{ACK}\) (2 góc tương ứng).

Hay \(\widehat{ABI}=\widehat{ACI}.\)

Xét 2 \(\Delta\) \(ABI\) và \(ACI\) có:

\(AB=AC\left(cmt\right)\)

\(\widehat{ABI}=\widehat{ACI}\left(cmt\right)\)

Cạnh AI chung

=> \(\Delta ABI=\Delta ACI\left(c-g-c\right)\)

=> \(\widehat{BAI}=\widehat{CAI}\) (2 góc tương ứng).

=> \(AI\) là tia phân giác của \(\widehat{A}\left(đpcm\right).\)

Chúc bạn học tốt!