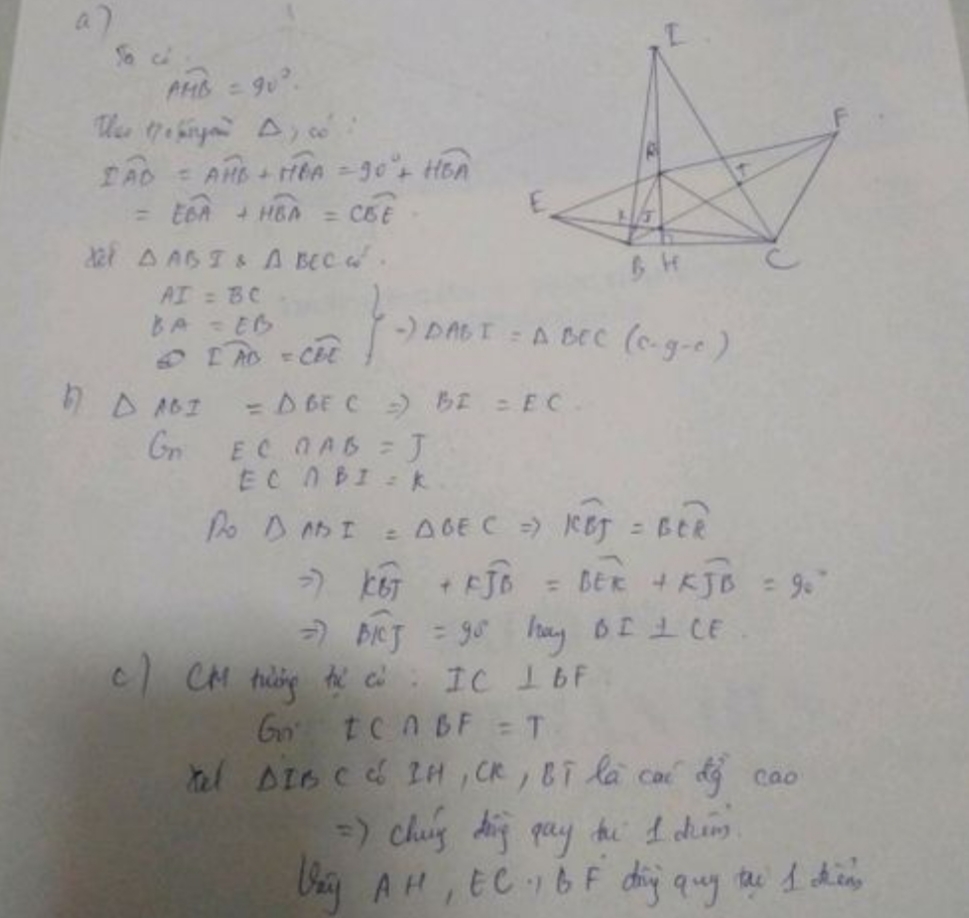Ôn tập cuối năm phần số học
Các câu hỏi tương tự
cho tam giác ABC vuông tại A có AB=6cm, AC=80cm, đường cao AH. Từ H vẽ HD và HE lần lượt vuông góc với AB và AC (D€AB,E€ AC) A) chứng minh AH=DE b) trên tia EC xác định điểm K sao cho EK=AE. Chứng minh tứ giác DHKE là hình bình hành.c) Tính đường cao AH
Câu 6 (3 điểm) Cho tam giác ABC nhọn có AB < AC. Kẻ 2 đường cao BE và CF cắt nhau tại H.
a) Chứng minh DABE ∽ DACF và AE. AC = AF. AB
b) Kẻ AH cắt BC tại D. Chứng minh AD vuông góc BC và góc ADF bằng góc ABH
cho ∆ABC nhọn, vẽ 3 đường cao BD,CE,AK cắt nhau tại I
a/ chứng minh ∆ADB đồng dạng ∆AEC
b/ chứng minh ∆EIB đồng dạng ∆DIC
c/ gọi J là giao điểm của DE và BC, lấy điểm M thuộc AK sao cho EM song song AC và cắt Ạ tại N, chứng minh EN bằng EM
C1: Giải PT sau: 2/x-1 = 1 + 2x/x+2 C2: Cho a < b, chứng tỏ: 2019 - 2018a > 2018 - 2018b C3: Cho hình thoi ABCD có AB = BD, qua c vẽ đường thẳng d bất kì.. đường thẳng này cắt tia đối của tia BA và DA lần lượt tại E và F. Gọi giao điểm của BF và DE là I a) C/m: tam giác BCE ~ tam giác DFC b) C/m: tam giác BDE ~ tam giác DFB c) Tính S đáy góc EIP=?
Cho ΔABC nhọn (AB AC) có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh: ΔABD ∼ ΔACE
b) Chứng minh: HD.HB HE.HC
c) AH cắt BC tại F. Kẻ FI vuông góc AC tại I. Chứng minh frac{IF}{IC} frac{FA}{FC}
d) Trên tia đối tia AF lấy điểm N sao cho AN AF. Gọi M là trung điểm cạnh IC. Chứng minh: NI ⊥ FM
P/s: Giải nhanh cho mình đi ạ, mình đang cần gấp. Không cần phải vẽ hình đâu ạ!
Đọc tiếp
Cho ΔABC nhọn (AB < AC) có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh: ΔABD ∼ ΔACE
b) Chứng minh: HD.HB = HE.HC
c) AH cắt BC tại F. Kẻ FI vuông góc AC tại I. Chứng minh \(\frac{IF}{IC}\) = \(\frac{FA}{FC}\)
d) Trên tia đối tia AF lấy điểm N sao cho AN = AF. Gọi M là trung điểm cạnh IC. Chứng minh: NI ⊥ FM
P/s: Giải nhanh cho mình đi ạ, mình đang cần gấp. Không cần phải vẽ hình đâu ạ!
Cho Delta ABC nhọn (AB AC) có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh:DeltaABD đồng dạng DeltaACE.
b) Chứng minh: HD.HBHE.HC
c)AH cắt BC tại F. Kẻ FI vuông góc AC tại I.Chứng minh:dfrac{IF}{IC}dfrac{FA}{FC}
d)Trên tia đối tia AF lấy điểm N sao cho AN AF. Gọi M là trung điểm cạnh IC.
Chứng minh: NI perpFM
Đọc tiếp
Cho \(\Delta\) ABC nhọn (AB < AC) có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh:\(\Delta\)ABD đồng dạng \(\Delta\)ACE.
b) Chứng minh: HD.HB=HE.HC
c)AH cắt BC tại F. Kẻ FI vuông góc AC tại I.Chứng minh:\(\dfrac{IF}{IC}=\dfrac{FA}{FC}\)
d)Trên tia đối tia AF lấy điểm N sao cho AN =AF. Gọi M là trung điểm cạnh IC.
Chứng minh: NI \(\perp\)FM
Cho tam giác ABC vuông tại A biết AB = 8 cm , AC = 6cm , CE là tia phân giác của góc ACB (E thuộc AB )
a) Tính độ dài đoạn thẳng AE
b) Kẻ AH vuông góc BC (H thuộc BC )
Chứng minh : ΔABC đồng dạng ΔHAC
c) Gọi F là giao điểm của CE và AH
Chứng minh: AE . CE = CE . HF
d)Từ B kẻ đường thẳng song song với CF cắt AF tại K.
CMR: AK = AB
Cho tam giác ABC vuông tại A có đường cao AH ( H thuộc BC)
a) Chứng minh : tam giác ABH đồng dạng tam giác CBA sau đó suy ra AB2= BH.BC
b) Chứng minh AH2=BH.CH
C) Gọi M là trung điểm của BH, kẻ CK vuông góc với AM tại K, CK cắt AH tại I. Chứng minh IA=IH
Cho tam giác AOB có AB = 18cm; OA = 12cm; OB = 9cm. Trên tia đối của tia OB lấy điểm D sao cho OD = 3cm. Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC
a) Tính độ dài OC; CD
b) Chứng minh rằng FD.BC = FC.AD
c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N. Cm: OM = ON