a) ĐKXĐ: \(\left\{{}\begin{matrix}a\ne1\\a\ge0\end{matrix}\right.\)
b) \(P=\frac{2a^2+4}{1-a^3}-\frac{1}{1+\sqrt{a}}-\frac{1}{1-\sqrt{a}}=\frac{2a^2+4}{\left(1-a\right)\left(1+a+a^2\right)}-\frac{\left(1+a+a^2\right)\left(1-\sqrt{a}\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}-\frac{\left(1+\sqrt{a}\right)\left(1+a+a^2\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{2a^2+4}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}-\frac{1-\sqrt{a}+a-a\sqrt{a}+a^2-a^2\sqrt{a}}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}-\frac{1+a+a^2+\sqrt{a}+a\sqrt{a}+a^2\sqrt{a}}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{2a^2+4-1+\sqrt{a}-a+a\sqrt{a}-a^2+a^2\sqrt{a}-1-a-a^2-\sqrt{a}-a\sqrt{a}-a^2\sqrt{a}}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{-2a+2}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{-2\left(a-1\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{2\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}=\frac{2}{a^2+a+1}\)








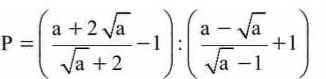 Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)
Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)

