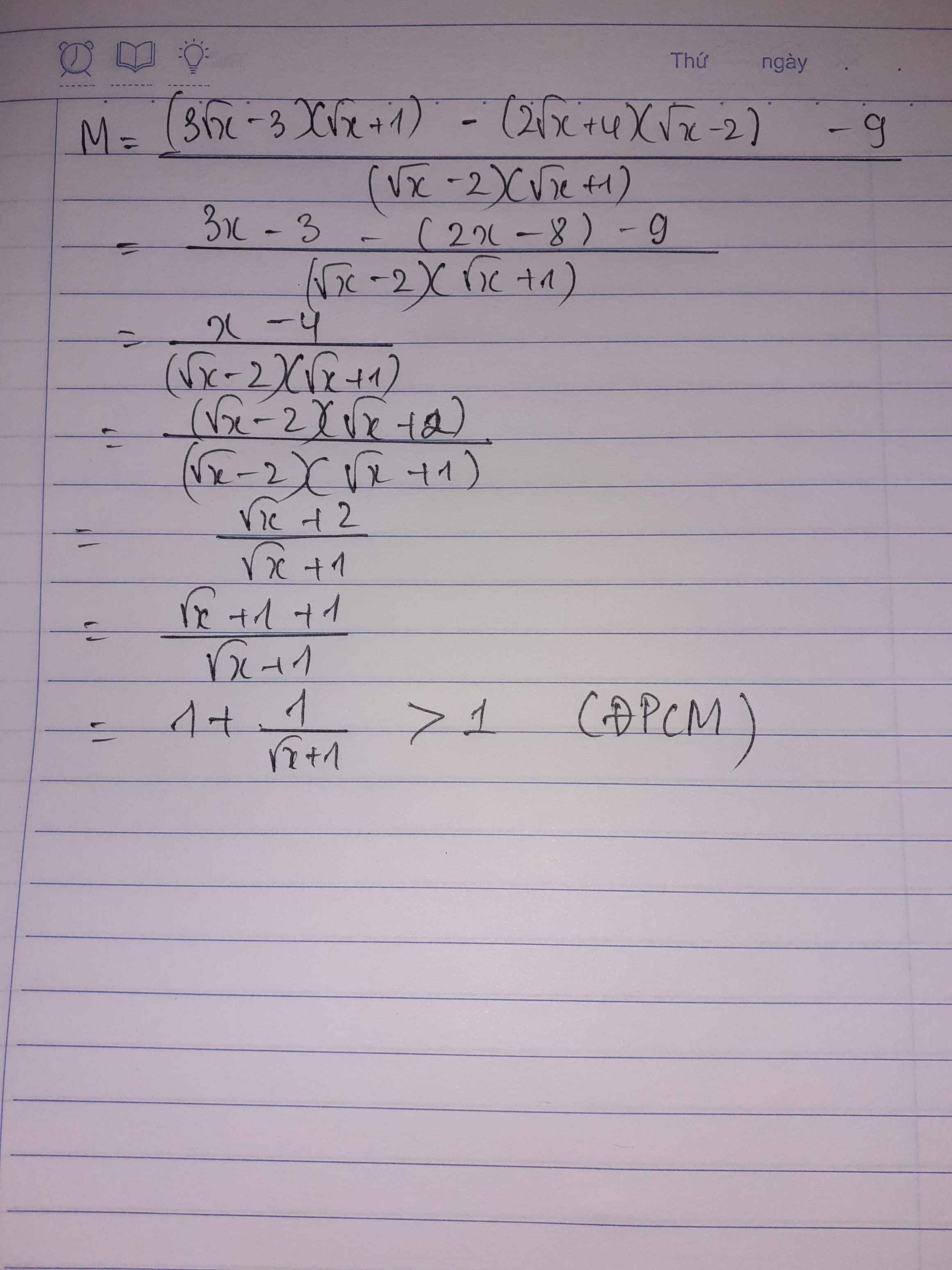Ta có: \(M=\dfrac{3\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+4}{\sqrt{x}+1}-\dfrac{9}{x-\sqrt{x}-2}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x-3-2x+8-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
Ta có: \(A-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-1\)
\(=\dfrac{\sqrt{x}+2-\sqrt{x}-1}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
hay A>1
\(M=\dfrac{3\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+4}{\sqrt{x}+1}-\dfrac{9}{x-\sqrt{x}-2}\\ =\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}-\dfrac{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{9}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{3\left(x-1\right)-2\left(x-4\right)-9}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}=\dfrac{x-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}>1\)