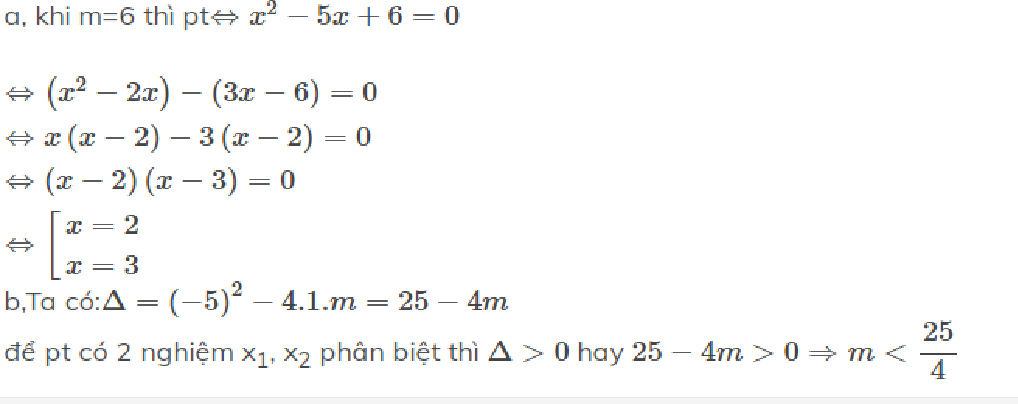Giải thích các bước giải:
a.Với m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}
b.Để phương trình có 2 nghiệm x1,x2x1,x2
a, khi m=6 thì pt\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
b,Ta có:\(\Delta=\left(-5\right)^2-4.1.m=25-4m\)
để pt có 2 nghiệm x1, x2 phân biệt thì \(\Delta>0\) hay \(25-4m>0\Rightarrow m< \dfrac{25}{4}\)