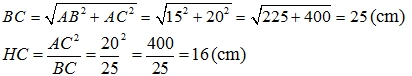Question

1.Cho tam giác ABC vuông tại A, có AB = 15cm, AC = 20cm. Vẽ đường cao AH (H∈BC).

a/ Chứng minh rằng   ΔHBA ~ ΔABC.

b/ Chứng  minh rằng AC² = BC.HC

c/ Tính độ dài các đoạn thẳng  BC, HC.

Answer 1

a)Xét tam giác HAB và tam giác ABC

góc ABC : chung

góc BHA=góc BAC=90^o

Suy ra: tam giác HAB ~ tam giác ABC (g-g)

b)Ta có: tam giác ABC vuông tại A

=>AC²=BC.HC (hệ thức lượng)

c)Ta có: \(BC^2=AB^2+AC^2=15^2+20^2=625\Rightarrow BC=25\left(cm\right)\)

Ta lại có: \(AC^2=BC.HC\left(HTL\right)\Rightarrow HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\left(cm\right)\)

Answer 2

a) Xét ΔHBA và ΔABC có:

∠BHA = ∠BAC = 90⁰ ( GT)

Góc B: Chung

Vậy ΔHBA  ~ ΔABC (g.g)

b) Xét ΔHAC và ΔABC.có:

∠AHC = ∠BAC =90⁰ ( GT)

Góc C : Chung

Vậy ΔHAC ~ ΔABC (g.g)

Suy ra:

c) Áp dụng định lí Pytago cho vuông tại A, ta có: