Question

1) Tìm 2 số x,y sao cho

2x-3y =1 và \(\frac{3x+2}{4}=\frac{y+5}{3}\)

2) Cho tam giác ABC cân tại A .Gọi M, N là 2 điểm lần lượt trên các cạnh AB,AC sao cho BM = CN .Chứng minh : MN song song với BC.

Answer 1

2)

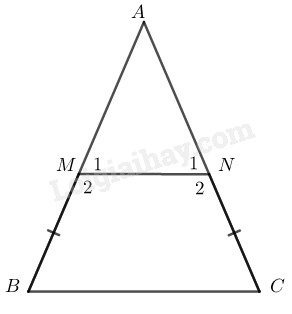
Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)

=> \(AB=AC.\)

Ta có:

\(\left\{{}\begin{matrix}AM+BM=AB\\AN+CN=AC\end{matrix}\right.\)

Mà \(\left\{{}\begin{matrix}BM=CN\left(gt\right)\\AB=AC\left(cmt\right)\end{matrix}\right.\)

=> \(AM=AN.\)

=> \(\Delta AMN\) cân tại A.

=> \(\widehat{M_1}=\widehat{N_1}\) (tính chất tam giác cân).

=> \(\widehat{M_1}=\widehat{N_1}=\frac{180^0-\widehat{A}}{2}\left(1\right).\)

Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)

=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).

=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\left(2\right).\)

Từ \(\left(1\right)và\left(2\right)\Rightarrow\widehat{M_1}=\widehat{B}.\)

Mà 2 góc này nằm ở vị trí đồng vị.

=> \(MN\) // \(BC\left(đpcm\right).\)

Chúc bạn học tốt!

Answer 2

~~~~~ Bài hình ~~~~~

Ta có: \(\left\{{}\begin{matrix}AM+MB=AB\\AN+NC=AC\end{matrix}\right.\)

\(Mà:\left\{{}\begin{matrix}AB=AC\left(\Delta ABCcân\right)\\MB=NC\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AM=AN\Rightarrow\Delta AMN\) cân.

\(\Rightarrow\widehat{AMN}=\widehat{ANM}=\frac{180^0-A}{2}\left(1\right)\)

Và \(\Delta ABC\) cân tại \(A\) nên:

\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)

Từ \(\left(1\right)\left(2\right)\Rightarrow\widehat{AMN}=\widehat{AMC}\)

Mà 2 góc đang ở vị trí đồng vị nên:

\(\Rightarrow MN//BC\left(đpcm\right)\)