\(P=log_{2x}x=\dfrac{1}{x}\cdot log_2x=\dfrac{1}{x}\cdot3=\dfrac{3}{x}\)
\(log_2x=3\Rightarrow log_x2=\dfrac{1}{3}\)
\(P=log_{2x}x=\dfrac{1}{log_x2x}=\dfrac{1}{log_x2+log_xx}=\dfrac{1}{\dfrac{1}{3}+1}=\dfrac{3}{4}\)
\(P=log_{2x}x=\dfrac{1}{x}\cdot log_2x=\dfrac{1}{x}\cdot3=\dfrac{3}{x}\)
\(log_2x=3\Rightarrow log_x2=\dfrac{1}{3}\)
\(P=log_{2x}x=\dfrac{1}{log_x2x}=\dfrac{1}{log_x2+log_xx}=\dfrac{1}{\dfrac{1}{3}+1}=\dfrac{3}{4}\)
Có bao nhiêu giá trị thực của tham số m để tập nghiệm của phương trình \(2^{x^2+x-2m}-2^{x^2-x-m+4}=2^{3x-m}-2^{x+4}\) có đúng hai phần tử?
Cho lg5=a . tính lg1\64 theo a?
A. 2+ 5a
B. 1-6a
C. 4-3a
D. 6(a-1)
Cho hai hàm số :
\(f\left(x\right)=\dfrac{a^x+a^{-x}}{2};g\left(x\right)=\dfrac{a^x-a^{-x}}{2}\)
a) Chứng minh rằng \(f\left(x\right)\) là hàm số chẵn, \(g\left(x\right)\) là hàm số lẻ
b) Tìm giá trị bé nhất của \(f\left(x\right)\) trên tập xác định
Giải các phương trình sau :
a) \(e^{2+\ln x}=x+3\)
b) \(e^{4-\ln x}=x\)
c) \(\left(5-x\right)\log\left(x-3\right)=0\)
Hai viên đạn cung roi khỏi nòng súng tai thoi điểm với những vận tốc khác nhau.viên đạn thứ nhất có vận tốc, viên đạn hai có vận tốc .hỏi từ giây thứ mấy thì viên đạn thứ nhất bay xa điểm xuất phát hơn viên đạn thứ hai
Giải phương trình :
\(2\log^2_2x-14\log_4x+3=0\)
Giải các phương trình sau :
a) \(9^x-3^x-6=0\)
b) \(e^{2x}-3e^x-4+12e^{-x}=0\)
c) \(3.4^x+\dfrac{1}{3}.9^{x+2}=6.4^{x+1}-\dfrac{1}{2}.9^{x+1}\)
d) \(2^{x^{ }-1}-3^{x^2}=3^{x^2-1}-2^{x^2+2}\)
Giải các bất phương trình :
a) \(2^{2x-1}+2^{2x-2}+2^{2x-3}\ge448\)
b) \(\left(0,4\right)^x-\left(2,5\right)^{x+1}>1,5\)
c) \(\log_3\left[\log_{\dfrac{1}{2}}\left(x^2-1\right)\right]< 1\)
d) \(\log^2_{0,2}x-5\log_{0,2}x< -6\)
câu 3, câu 4 thôi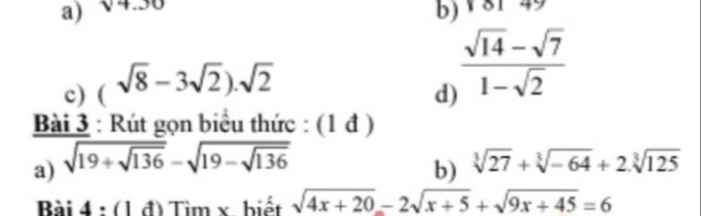
Có bao nhiêu giá trị nguyên m để phương trình 20212x - 22. 2021x + 2021 - m= 0 có 2 nghiệm x1, x2 thỏa mãn: x1 + x2 ≥ \(\dfrac{1}{2}\)