\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(\Rightarrow x^2+y^2-z^2=-2xy\)
Tương tự: \(\left\{{}\begin{matrix}y^2+z^2-x^2=-2yz\\z^2+x^2-y^2=-2zx\end{matrix}\right.\)
\(A=\dfrac{xy}{x^2+y^2-z^2}+\dfrac{yz}{y^2+z^2-x^2}+\dfrac{zx}{z^2+x^2-y^2}\)
\(=-\left(\dfrac{xy}{2xy}+\dfrac{yz}{2yz}+\dfrac{zx}{2zx}\right)=-\dfrac{3}{2}\)
Tìm gtnn của
P= 10x2 - 6x + 2 / x2 + 1
Trung bình cộng các giá trị x thỏa mãn: 4(x-1)2=x2
cho b.thức \(\dfrac{1-3x}{2x}+\dfrac{3x-2}{2x-1}+\dfrac{3x-2}{2x-4x^2}\)
hãy tính rút gọn rồi tính giá trị của b.thức tại x=\(\dfrac{1}{966}\)
CVT là gì?
xin mn đừng lm tắt nhó
Tìm x biết:
a, \(ax-x+1=a^2\) \(\left(a\ne1\right)\)
b, \(a^2x+x=2a^2-3\)
c, \(a^2x+3ax+9=a^2\) \(\left(a\ne0;a\ne-3\right)\)
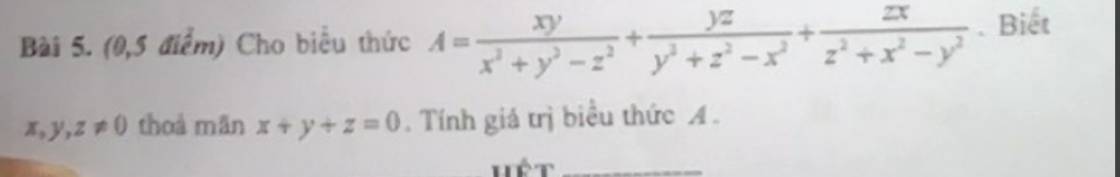
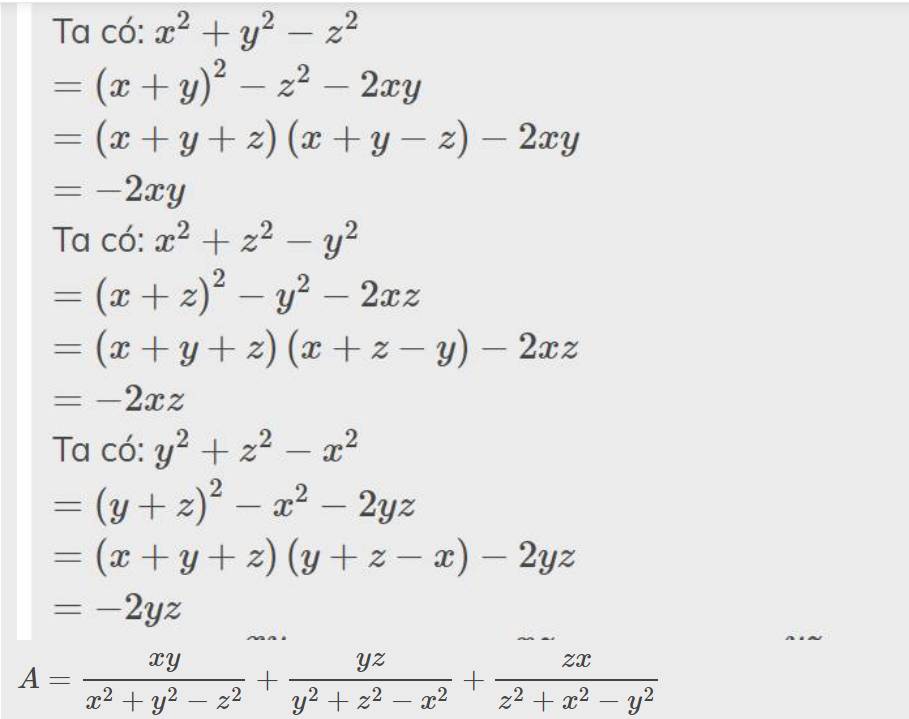
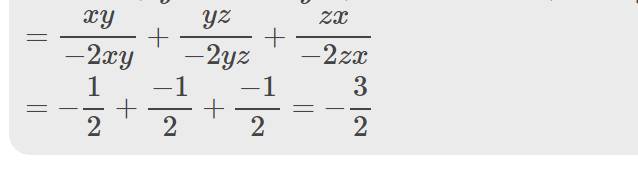
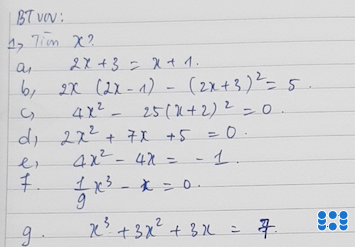
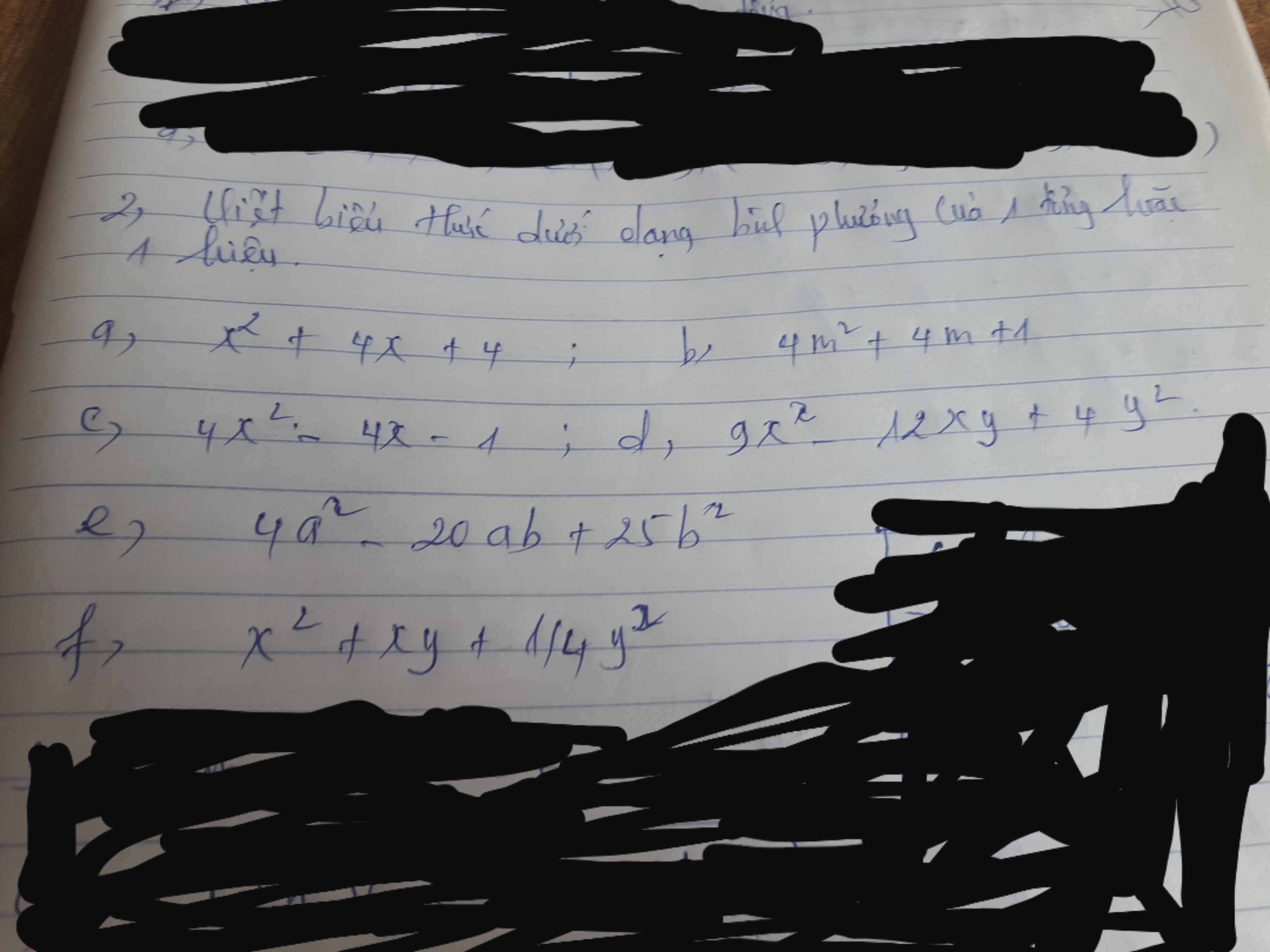
giải thích giùm mình với
