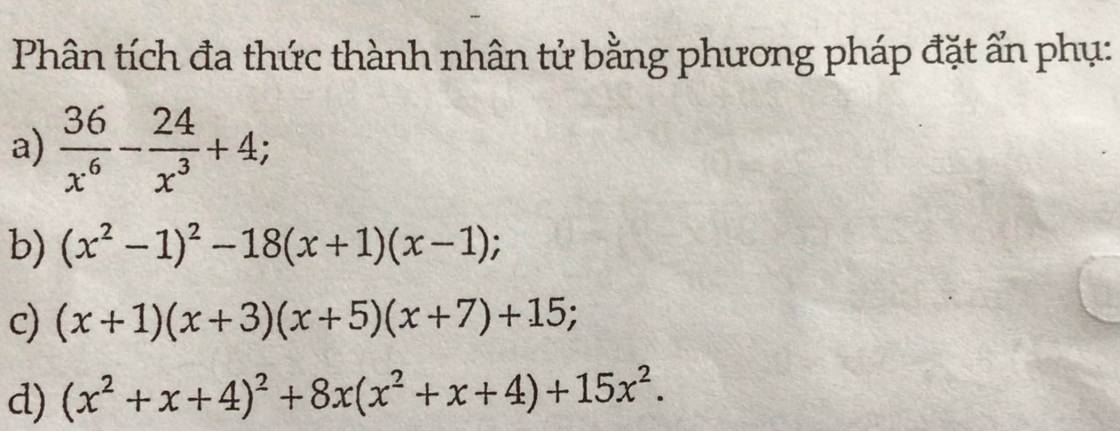b: (x^2-1)^2-18(x+1)(x-1)
=(x+1)^2*(x-1)^2-18(x+1)(x-1)
=(x+1)(x-1)(x^2-1-18)
=(x+1)(x-1)(x^2-19)
c: (x+1)(x+3)(x+5)(x+7)+15
=(x^2+8x+7)(x^2+8x+15)+15
=(x^2+8x)^2+22(x^2+8x)+120
=(x^2+8x+10)(x^2+8x+12)
=(x^2+8x+10)(x+2)(x+6)
d: (x^2+x+4)^2+8x(x^2+x+4)+15x^2
=(x^2+x+4)^2+3x(x^2+x+4)+5x(x^2+x+4)+15x^2
=(x^2+x+4+3x)(x^2+x+4+5x)
=(x^2+6x+4)(x^2+4x+4)
=(x^2+6x+4)(x+2)^2
a: \(\dfrac{36}{x^6}-\dfrac{24}{x^3}+4\)
\(=4\left(\dfrac{9}{x^6}-\dfrac{6}{x^3}+1\right)\)
\(=4\left[\left(\dfrac{3}{x^3}\right)^2-2\cdot\dfrac{3}{x^3}\cdot1+1^2\right]\)
\(=4\cdot\left(\dfrac{3}{x^3}-1\right)^2\)
\(a,\dfrac{36}{x^6}-\dfrac{24}{x^3}+4\\ =4\left(\dfrac{9}{x^6}-\dfrac{6}{x^3}+1\right)\\ =4\left[\left(\dfrac{3}{x^3}\right)^2-2\cdot\dfrac{3}{x^3}\cdot1+1^2\right]\\ =4\left(\dfrac{3}{x^3}-1\right)^2\)
\(b,\left(x^2-1\right)^2-18\left(x+1\right)\left(x-1\right)\\ =\left(x^2-1\right)\left(x^2-1\right)-18\left(x^2-1\right)\\ =\left(x^2-1\right)\left(x^2-1-18\right)\\ =\left(x^2-1\right)\left(x^2-19\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2-19\right)\)
\(c,\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\\ =\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\\ =\left[\left(x^2+8x+11\right)-4\right]\left[\left(x^2+8x+11\right)+4\right]+15\\ =\left(x^2+8x+11\right)^2-16+15\\ =\left(x^2+8x+11\right)^2-1\\ =\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)
\(d,\left(x^2+x+4\right)^2+8x\left(x^2+x+4\right)+15x^2\\ =\left(x^2+x+4\right)^2+3x\left(x^2+x+4\right)+5x\left(x^2+x+4\right)+15x^2\\ =\left(x^2+x+4\right)\left(x^2+4x+4\right)+5x\left(x^2+4x+4\right)\\ =\left(x^2+4x+4\right)\left(x^2+6x+4\right)\\ =\left(x+2\right)^2\left(x^2+6x+4\right)\)