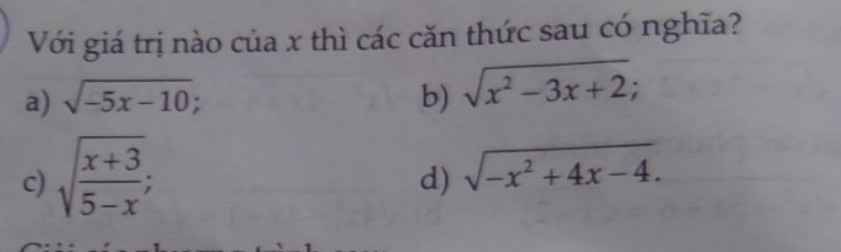\(a,\)
Biểu thức \(\sqrt{-5x-10}\) có nghĩa khi:
\(-5x-10\ge0\)
\(\Leftrightarrow5x\le-10\)
\(\Leftrightarrow x\le-2\)
Vậy \(x\le-2\).
\(b,\)
Biểu thức \(\sqrt{x^2-3x+2}\) có nghĩa khi:
\(x^2-3x+2\ge0\)
\(\Leftrightarrow x^2-x-2x+2\ge0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2\ge0\\x-1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-2\le0\\x-1\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\x\ge1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le2\\x\le1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le1\end{matrix}\right.\)
Vậy \(x\ge2\) hoặc \(x\le1\).
\(c,\)
Biểu thức \(\sqrt{\dfrac{x+3}{5-x}}\) có nghĩa khi:
\(\dfrac{x+3}{5-x}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3\ge0\\5-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3\le0\\5-x< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-3\\x< 5\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-3\\x>5\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-3\le x< 5\\5< x\le-3\left(\text{vô lí}\right)\end{matrix}\right.\)
Vậy \(-3\le x< 5\).
\(d,\)
Biểu thức \(\sqrt{-x^2+4x-4}\) có nghĩa khi:
\(-x^2+4x-4\ge0\)
\(\Leftrightarrow x^2-4x+4\le0\)
\(\Leftrightarrow\left(x-2\right)^2\le0\left(1\right)\)
Ta thấy:
\(\left(x-2\right)^2\ge0\forall x\in R\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy \(x=2\).