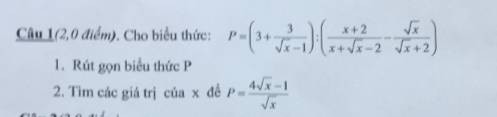\(1,P=\left(3+\dfrac{3}{\sqrt{x}-1}\right):\left(\dfrac{x+2}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\right)\)\(\left(dkxd:x\ge0,x\ne4,x\ne1\right)\)
\(=\dfrac{3\left(\sqrt{x}-1\right)+3}{\sqrt{x}-1}:\dfrac{\left(x+2\right)\left(\sqrt{x}+2\right)-\sqrt{x}\left(x+\sqrt{x}-2\right)}{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-3+3}{\sqrt{x}-1}.\dfrac{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{x\sqrt{x}+2x+2\sqrt{x}+4-x\sqrt{x}-x+2\sqrt{x}}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-1}.\dfrac{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{x+4\sqrt{x}+4}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-1}.\dfrac{\left(x-\sqrt{x}+2\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-1}.\dfrac{\left[\sqrt{x}\left(\sqrt{x}-1\right)+2\left(\sqrt{x}-1\right)\right]}{\sqrt{x}+2}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-1}.\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+2}\)
\(=3\sqrt{x}\)
\(2,P=\dfrac{4\sqrt{x}-1}{\sqrt{x}}\)
\(\Rightarrow\dfrac{4\sqrt{x}-1}{\sqrt{x}}=3\sqrt{x}\)
\(\Rightarrow\dfrac{4\sqrt{x}-1-3\sqrt{x}.\sqrt{x}}{\sqrt{x}}=0\)
\(\Rightarrow4\sqrt{x}-1-2x=0\)
\(\Rightarrow4\sqrt{x}=2x+1\)
Bình phương 2 vế pt, ta có :
\(16x=\left(2x+1\right)^2\)
\(\Rightarrow16x=4x^2+4x+1\)
\(\Rightarrow-4x^2+12x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+2\sqrt{2}}{2}\\x=\dfrac{3-2\sqrt{2}}{2}\end{matrix}\right.\)
Thay lần lượt các giá trị trên vào pt, ta thấy thỏa.
Vậy giá trị của \(x=\dfrac{3+2\sqrt{2}}{2};x=\dfrac{3-2\sqrt{2}}{2}\) thì \(P=\dfrac{4\sqrt{x}-1}{\sqrt{x}}\)