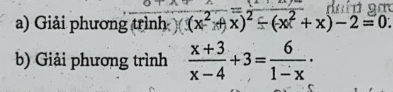a.
Đặt \(x^2+x=t\Rightarrow t^2-t-2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x=-1\\x^2+x=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\\x^2+x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vn\right)\\\left(x-1\right)\left(x+2\right)=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
b.
ĐKXĐ: \(x\ne\left\{1;4\right\}\)
\(\dfrac{x+3}{x-4}+3+\dfrac{6}{x-1}=0\)
\(\Leftrightarrow\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x-4\right)}+\dfrac{3\left(x-1\right)\left(x-4\right)}{\left(x-1\right)\left(x-4\right)}+\dfrac{6\left(x-4\right)}{\left(x-1\right)\left(x-4\right)}=0\)
\(\Rightarrow\left(x+3\right)\left(x-1\right)+3\left(x-1\right)\left(x-4\right)+6\left(x-4\right)=0\)
\(\Leftrightarrow4x^2-7x-15=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{4}\end{matrix}\right.\) (thỏa mãn)