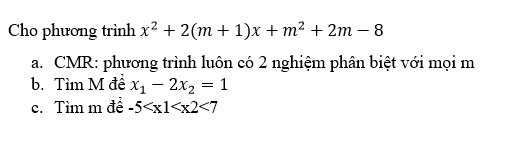\(a;\Delta'=\left(m+1\right)^2-\left(m^2+2m-8\right)=m^2+2m+1-m^2-2m+8=9>0\)
\(\Rightarrowđpcm\)
\(b,\left\{{}\begin{matrix}x1+x2=-2\left(m+1\right)\\x1-2x2=1\\x1.x2=m^2+2m-8\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x1=1+2x2=1+\dfrac{-2m-3}{3}=\dfrac{-2m}{3}\\x2=\dfrac{-2m-3}{3}\\\left(-\dfrac{2m}{3}\right)\left(\dfrac{-2m-3}{3}\right)=m^2+2m-8\Leftrightarrow\dfrac{2m\left(2m+3\right)}{9}=m^2+2m=8\left(1\right)\end{matrix}\right.\)
\(giải\left(1\right)\Rightarrow m=....\)
\(c,-5< x1< x2< 7\Leftrightarrow\left\{{}\begin{matrix}-5< x1< x2\left(1\right)\\x1< x2< 7\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x1+5\right)\left(x2+5\right)>0\\x1+x2+10>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x1x2+5\left(x1+x2\right)+25>0\\-2\left(m+1\right)+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-8-10\left(m+1\right)+25>0\\m< 4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 1\\m>7\end{matrix}\right.\\m< 4\end{matrix}\right.\)\(\Leftrightarrow m< 1\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x1-7\right)\left(x2-7\right)>0\\x1+x2-14< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x1x2-7\left(x1+x2\right)+49>0\\-2\left(m+1\right)-14< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-8+14\left(m+1\right)+49>0\\m>-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -11\\m>-5\end{matrix}\right.\\m>-4\end{matrix}\right.\)
\(\Leftrightarrow m>-4\)
\(\Rightarrow-4< m< 1\) \(thì-5< x1< x2< 7\)