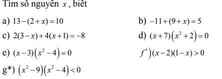a: 13-(2+x)=10
=>x+2=13-10=3
=>x=3-2=1
b: -11+(9+x)=5
=>x+9=5+11=16
=>x=16-9=7
c: 2(3-x)+4(x+1)=-8
=>6-2x+4x+4=-8
=>2x+10=-8
=>2x=-18
=>x=-9
d: (x+7)(x^2+2)=0
mà \(x^2+2>=2>0\forall x\)
nên x+7=0
=>x=-7
e: \(\left(x-3\right)\left(x^2-4\right)=0\)
=>\(\left(x-3\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\end{matrix}\right.\)
f: \(\left(x-2\right)\left(1-x\right)>0\)
=>(x-2)(x-1)<0
TH1: \(\left\{{}\begin{matrix}x-2>0\\x-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>2\\x< 1\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-2< 0\\x-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 2\\x>1\end{matrix}\right.\)
=>1<x<2
g) (x^2-9)(x^2-4)<0
TH1: \(\left\{{}\begin{matrix}x^2-9>0\\x^2-4< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2>9\\x^2< 4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>3\\x< -3\end{matrix}\right.\\-2< x< 2\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x^2-9< 0\\x^2-4>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2< 9\\x^2>4\end{matrix}\right.\)
=>\(4< x^2< 9\)
=>\(\left[{}\begin{matrix}-2>x>-3\\2< x< 3\end{matrix}\right.\)