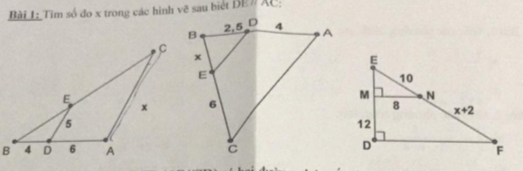
a, Theo hệ quả Ta lét \(\dfrac{BD}{AB}=\dfrac{DE}{AC}\Rightarrow\dfrac{4}{10}=\dfrac{5}{x}\Rightarrow x=\dfrac{10.5}{4}=\dfrac{50}{4}\)
b, Theo định lí Ta lét
\(\dfrac{BE}{EC}=\dfrac{BD}{DA}\Rightarrow\dfrac{x}{6}=\dfrac{2,5}{4}\Rightarrow x=\dfrac{6.2,5}{4}=\dfrac{15}{4}\)
c, Theo định lí Pytago tam giác EMN vuông tại M
\(ME=\sqrt{EN^2-MN^2}=6\)
Theo định lí Ta lét \(\dfrac{6}{12}=\dfrac{10}{x+2}\Rightarrow6x+12=120\Leftrightarrow x=18\)
hình 1. ta có: DE // AC ( bạn thiếu điều kiện nha nên mik cho )
áp dụng định lý ta lét:
\(\Rightarrow\dfrac{DE}{AC}=\dfrac{BD}{DA}\)
\(\Leftrightarrow\dfrac{5}{x}=\dfrac{4}{6}\)
\(\Leftrightarrow4x=24\Leftrightarrow x=6\)
hình 2. ta có: ED // AC ( bạn lại thiếu điều kiện )
Áp dụng định lý ta lét:
\(\Rightarrow\dfrac{BE}{CE}=\dfrac{BD}{AD}\)
\(\Leftrightarrow\dfrac{x}{6}=\dfrac{2,5}{4}\)
\(\Leftrightarrow4x=15\)
\(\Leftrightarrow x=3,75\)
c.áp dụng định lý pitago vào tam giác vuông EMN:
\(\Rightarrow EM=6\)
ta có: MN // DF ( cùng vuông với ED )
Áp dụng định lý ta lét
\(\Rightarrow\dfrac{EM}{DM}=\dfrac{EN}{NF}\)
\(\Leftrightarrow\dfrac{6}{12}=\dfrac{10}{x+2}\)
\(\Leftrightarrow6\left(x+2\right)=120\)
\(\Leftrightarrow x+2=20\)
\(\Leftrightarrow x=18\)