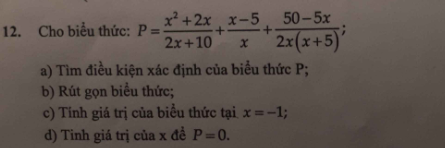a, ĐKXĐ:\(\left\{{}\begin{matrix}2x+10\ne0\\x\ne0\\2x\left(x+5\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-5\\x\ne0\\2x\left(x+5\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-5\\x\ne0\end{matrix}\right.\)
b, \(P=\dfrac{x^2+2x}{2x+10}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x\left(x^2+2x\right)}{2x\left(x+5\right)}+\dfrac{2\left(x-5\right)\left(x+5\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2x^2-50}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x\left(x^2+5x-x-5\right)}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x\left[x\left(x+5\right)-\left(x+5\right)\right]}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}\)
\(\Leftrightarrow P=\dfrac{x-1}{2}\)
c, Thay x=-1 vào P ta có:\(P=\dfrac{x-1}{2}=\dfrac{-1-1}{2}=\dfrac{-2}{2}=-1\)
d, Để P=0 thì \(\dfrac{x-1}{2}=0\Leftrightarrow x-1=0\Leftrightarrow x=1\left(tm\right)\)
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(P=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Thay x=-1 vào P, ta đc:
P=-2/2=-1