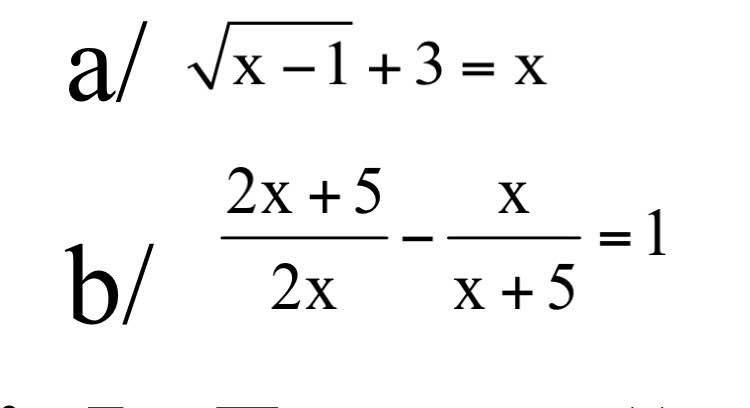b: \(\Leftrightarrow\left(2x+5\right)\left(x+5\right)-2x^2=2x\left(x+5\right)\)
\(\Leftrightarrow2x^2+10x+5x+25-2x^2-2x^2-10x=0\)
\(\Leftrightarrow-2x^2+5x+25=0\)
\(\Leftrightarrow2x^2-5x-25=0\)
\(\Rightarrow2x^2-10x+5x-25=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-5\right)=0\)
hay \(x\in\left\{-\dfrac{5}{2};5\right\}\)
a, ĐKXĐ:\(x\ge1\)
\(\sqrt{x-1}+3=x\\ \Leftrightarrow\sqrt{x-1}=x-3\left(x\ge3\right)\\ \Leftrightarrow x-1=x^2-6x+9\\ \Leftrightarrow x^2-7x+10=0\\ \Leftrightarrow\left(x-2\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=5\left(tm\right)\end{matrix}\right.\)
b, ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne-5\end{matrix}\right.\)
\(\dfrac{2x+5}{2x}-\dfrac{x}{x+5}=1\\ \Leftrightarrow\dfrac{\left(2x+5\right)\left(x+5\right)-2x^2}{2x\left(x+5\right)}=1\\ \Leftrightarrow2x^2+5x+10x+25-2x^2=2x^2+10x\\ \Leftrightarrow2x^2-5x-25=0\\ \Leftrightarrow\left(2x+5\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\left(tm\right)\\x=5\left(tm\right)\end{matrix}\right.\)