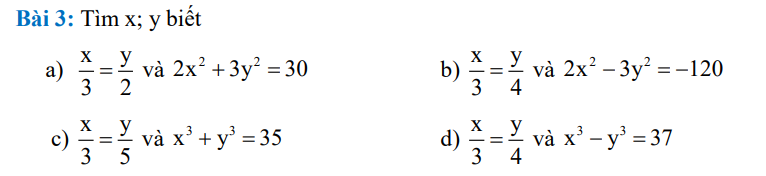a) \(\dfrac{x}{3}\)=\(\dfrac{y}{2}\)=>\(\dfrac{x^2}{9}\)=\(\dfrac{y^2}{4}\)=>\(\dfrac{2x^2+3y^2}{18+12}\)=\(\dfrac{30}{30}\)=1
Vậy => x= \(\overset{+}{-}\)3 , y= \(\overset{+}{-}\)2
b. \(\dfrac{x}{3}=\dfrac{y}{4}=>\dfrac{x^2}{9}=\dfrac{y^2}{16}=>\dfrac{2x^2-3y^2}{9-16}=\dfrac{120}{7}\)
=> x = 360/7 ; y = 480/7
c.\(\dfrac{x}{3}=\dfrac{y}{5}=>\dfrac{x^3}{27}=\dfrac{y^3}{125}=>\dfrac{x^3+y^3}{27+125}=\dfrac{35}{152}\)
=> x = 105/152 ; y = 175/152
d: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)
Ta có: \(x^3-y^3=37\)
\(\Leftrightarrow27k^3-64k^3=37\)
\(\Leftrightarrow k=-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)