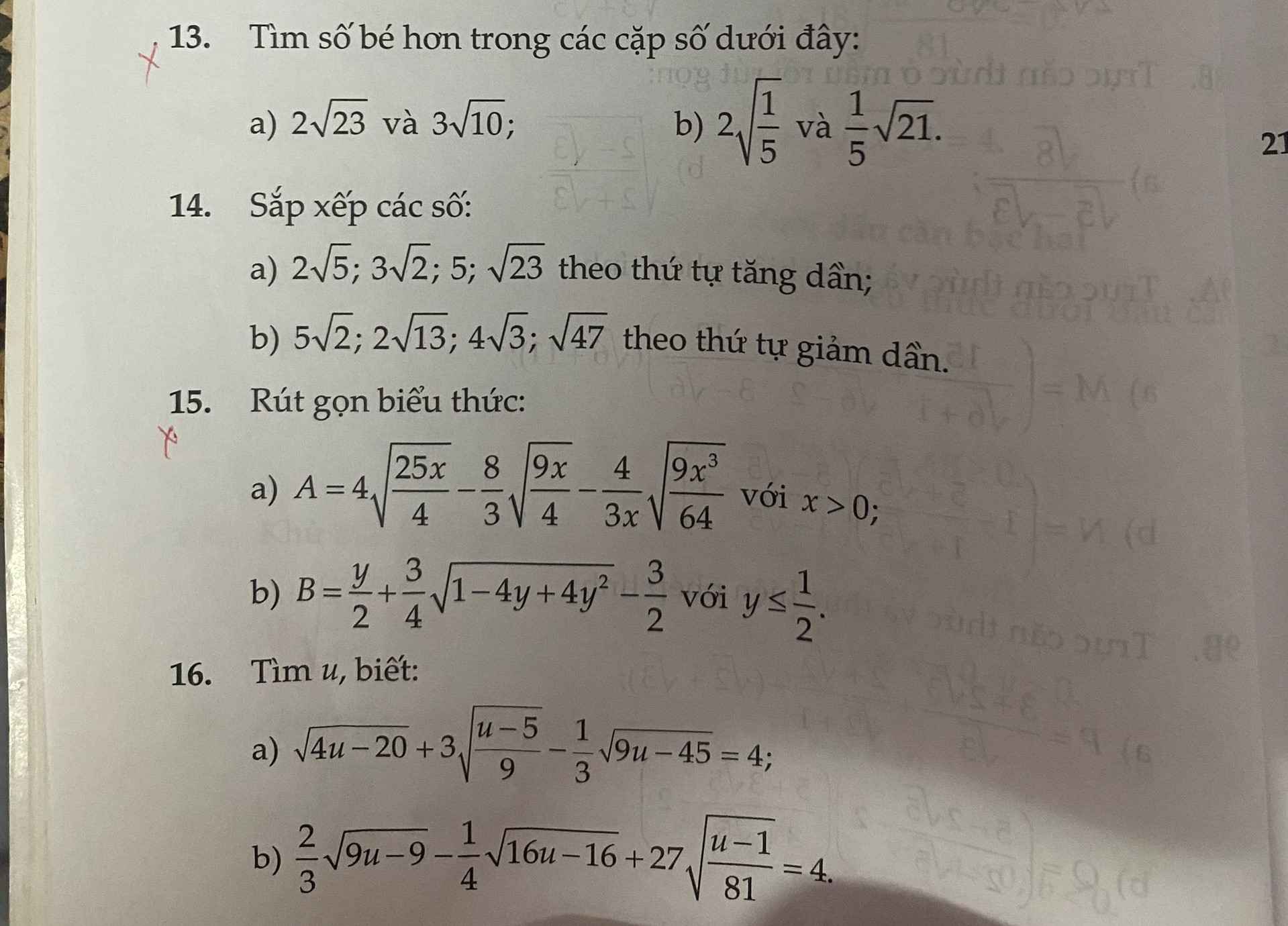a) \(2\sqrt{23}=\sqrt{4}.\sqrt{23}=\sqrt{4.23}=\sqrt{92}\)
\(3\sqrt{10}=\sqrt{9}.\sqrt{10}=\sqrt{90}\)
Vì \(92>90\Rightarrow\sqrt{92}>\sqrt{90}\Rightarrow2\sqrt{23}>3\sqrt{10}\)
b) \(2\sqrt{\dfrac{1}{5}}=\sqrt{\dfrac{1}{5}.4}=\sqrt{\dfrac{4}{5}}=\sqrt{\dfrac{20}{25}}\)
\(\dfrac{1}{5}\sqrt{21}=\sqrt{\dfrac{1}{25}.21}=\sqrt{\dfrac{21}{25}}\)
Vì \(\dfrac{20}{25}< \dfrac{21}{25}\Rightarrow\sqrt{\dfrac{20}{25}}< \sqrt{\dfrac{21}{25}}\Rightarrow2\sqrt{\dfrac{1}{5}}< \dfrac{1}{5}\sqrt{21}\)
Bài 16:
a: Ta có: \(\sqrt{4u-20}+3\sqrt{\dfrac{u-5}{9}}-\dfrac{1}{3}\sqrt{9u-45}=4\)
\(\Leftrightarrow2\sqrt{u-5}+3\cdot\dfrac{\sqrt{u-5}}{3}-\dfrac{1}{3}\cdot3\sqrt{u-5}=4\)
\(\Leftrightarrow u-5=4\)
hay u=9
b: Ta có: \(\dfrac{2}{3}\sqrt{9u-9}-\dfrac{1}{4}\sqrt{16u-16}+27\sqrt{\dfrac{u-1}{81}}=4\)
\(\Leftrightarrow2\sqrt{u-3}-4\sqrt{u-3}+3\sqrt{u-1}=4\)
\(\Leftrightarrow u-3=16\)
hay u=19