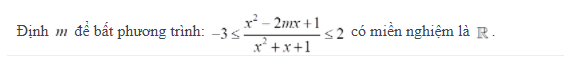Question

Answer 1

Do \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x nên BPT tương đương:

\(-3\left(x^2+x+1\right)\le x^2-2mx+1\le2\left(x^2+x+1\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2\left(m+1\right)x+1\ge0\\4x^2-\left(2m-3\right)x+4\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta_1'=\left(m+1\right)^2-1\le0\\\Delta_2=\left(2m-3\right)^2-64\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-2\le m\le0\\-\dfrac{5}{2}\le m\le\dfrac{11}{2}\end{matrix}\right.\) \(\Rightarrow-2\le m\le0\)