a) Ta có : \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)

\(\Rightarrow\dfrac{a}{2}=\dfrac{2b}{6}=\dfrac{3c}{12}=\dfrac{a+2b+3c}{2+6+12}=\dfrac{-20}{20}=-1\)

\(\Rightarrow\left\{{}\begin{matrix}a=\left(-1\right)\cdot2=-2\\b=\dfrac{\left(-1\right).6}{2}=-3\\c=\dfrac{\left(-1\right).12}{3}=-4\end{matrix}\right.\)

b) Ta có : \(S=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\)

\(=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(=1-\dfrac{1}{100}=\dfrac{99}{100}\).

Vậy : \(S=\dfrac{99}{100}.\)

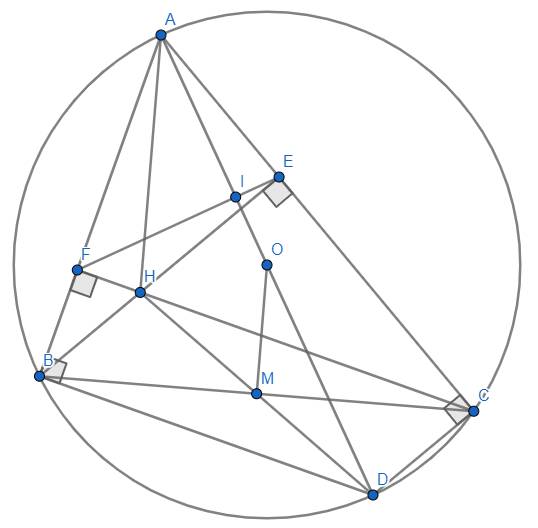
a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).

Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).

Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).

b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)

Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)

Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.

Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.

c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)

Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).

Và : \(BE\perp AC\left(gt\right)\)

Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)

Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.

Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)

Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).

Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).

d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).

Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).

Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)

Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)

Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)

\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)

\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)

\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)

\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)

\(\Rightarrow OA\perp EF\) (đpcm).

a) Điều kiện : \(m\notin\left\{0;3\right\}\)

Phương trình hoành độ giao điểm của \(\left(d\right),\left(d'\right)\) : \(mx+7=3x+m^2-2\).

Do giao điểm của hai đường thẳng nằm trên trục tung nên giá trị hoành độ của điểm đó bằng 0, tức \(x=0\). Thay vào phương trình ta được : \(7=m^2-2\)

\(\Leftrightarrow m^2=9\Leftrightarrow\left[{}\begin{matrix}m=3\left(loại\right)\\m=-3\left(nhận\right)\end{matrix}\right.\)

Vậy : \(m=-3\).

a) a₁. Chứng minh \(BAOE\) là tứ giác nội tiếp.

Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).

a₂. Chứng minh : \(BH.BO=BD.BC\).

Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)

\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)

Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)

\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)

\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)

Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).

b) b₁. Chứng minh \(DHOC\) là tứ giác nội tiếp.

Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)

Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)

Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)

Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).

b₂. Chứng minh : \(\hat{BHD}=\hat{OHC}\).

Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).

Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)

Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)

Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).

c) Chưa nghĩ ra ạ:)

Xét \(\Delta DCH,\Delta CBA\) có : \(\left\{{}\begin{matrix}\hat{CDH}=\hat{ACB}=90^o\left(gt\right)\\\hat{DCH}=\hat{CBA}\left(\text{cùng phụ với góc A}\right)\end{matrix}\right.\)

\(\Rightarrow\Delta DCH\sim\Delta CBA\left(g.g\right)\) (đpcm).

\(\Rightarrow\dfrac{DH}{AC}=\dfrac{CD}{BC}\)

Ta cũng có : \(BD\) là phân giác nên : \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}\)

Suy ra : \(\dfrac{DH}{AC}=\dfrac{AD}{AB}\Rightarrow AD.AC=DH.AB\) (đpcm).

Gọi \(x\) với đơn vị là \(km\) là độ dài quãng đường \(AB\left(x>0\right)\).

Thời gian đi của người đó là : \(\dfrac{x}{25}\left(h\right)\)

Thời gian về của người đó là :\(\dfrac{x}{30}\left(h\right)\).

Do thời gian về ít hơn thời gian đi là \(20\left(phút\right)=\dfrac{1}{3}\left(h\right)\) nên ta có phương trình : 

\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\) \(\Leftrightarrow\dfrac{x}{150}=\dfrac{1}{3}\Leftrightarrow x=50\) (thỏa mãn).

Vậy : Quãng đường AB dài 50km.

Phương trình hoành độ giao điểm của \(\left(d\right),\left(P\right)\) là : \(x^2=\left(2m+1\right)x-2m\)

hay : \(x^2-\left(2m+1\right)x+2m=0\left(I\right)\).

Do, \(\left(d\right)\cap\left(P\right)\) tại hai điểm phân biệt nên phương trình \(\left(I\right)\) có hai nghiệm phân biệt khi \(\Delta=b^2-4ac>0\)

Hay : \(\left[-\left(2m+1\right)\right]^2-4.1.2m>0\)

\(\Leftrightarrow4m^2+4m+1-8m>0\)

\(\Leftrightarrow\left(2m-1\right)^2>0\Rightarrow m\ne\dfrac{1}{2}\).

Theo định lí Vi-ét : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(2m+1\right)}{1}=2m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{2m}{1}=2m\end{matrix}\right.\)

Theo đề bài : \(y_1+y_2-x_1x_2=1\left(II\right)\)

Do các điểm trên thuộc \(\left(P\right)\) nên \(\left\{{}\begin{matrix}y_1=x_1^2\\y_2=x_2^2\end{matrix}\right.\).

Khi đó, ta viết lại phương trình \(\left(II\right)\) thành : \(x_1^2+x_2^2-x_1x_2=1\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=1\)

\(\Rightarrow\left(2m+1\right)^2-3.2m=1\)

\(\Leftrightarrow4m^2+4m+1-6m=1\)

\(\Leftrightarrow4m^2-2m=0\)

\(\Leftrightarrow2m\left(2m-1\right)=0\Leftrightarrow\left[{}\begin{matrix}2m=0\\2m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)

Vậy : \(m=0\).

\(y_1+y_2-x_1x_2\) bằng cái gì vậy bạn ?