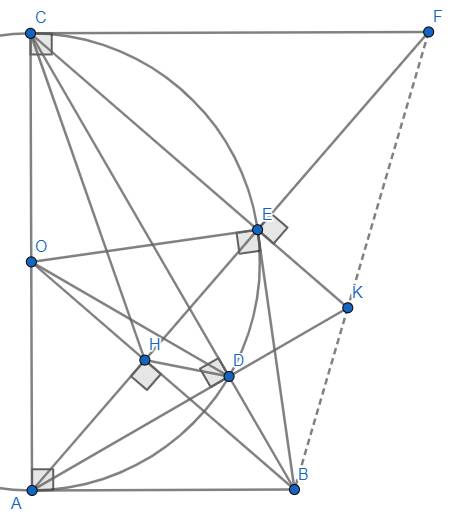
Cho tam giác ABC vuông tại A có AB < AC. Trên nửa mặt phẳng bờ là đường thẳng AC chứa điểm B vẽ nửa đường tròn (O) đường kính AC, nửa đường tròn này cắt BC tại D. Vẽ tiếp tuyến BE của nửa đường tròn (O)(với E là tiếp điểm, E khác 4). BO cắt AE tại điểm H . a) Chứng minh BAOE nội tiếp và BH.BO = BD.BC. b) Chứng minh DHOC là tứ giác nội tiếp và BHD=OHC. c) Tiếp tuyến tại C của nửa đường tròn (O) cắt AE tại F, AD cắt CE tại K. Chứng minh ba điểm B,K,F thẳng hàng.
a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)