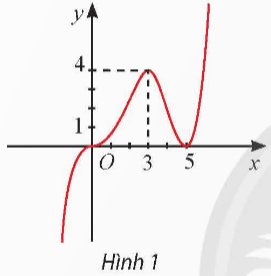
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng
A. (5; + ∞). B. (3; 5).
C. (0; 5). D. (3; + ∞).
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng
A. (5; + ∞). B. (3; 5).
C. (0; 5). D. (3; + ∞).

Cho hàm số y = f(x) có đồ thị như Hình 1.
Hàm số đạt cực đại tại
A. x = 0. B. x = 3.
C. x = 4. D. x = 5.

Thảo luận (1)Hướng dẫn giảiChọn B
Từ hình vẽ ta thấy, qua điểm x = 3 thì hàm số chuyển từ đồng biến sang nghịch biến
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số \(y=\dfrac{x^2-4x+1}{x-4}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.
B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.
C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.
D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.
Thảo luận (1)Hướng dẫn giảiChọn B
\(y' = \frac{{{x^2} - 8x + 15}}{{{{(x - 4)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 5\end{array} \right.\)
Bảng biến thiên:
Từ bảng biến thiên ta thấy, hàm số đạt cực đại tại x = 3 và \({y_{cd}} = 2\), đạt cực tiểu tại x = 5 và \({y_{ct}} = 6\)
(Trả lời bởi Nguyễn Quốc Đạt)
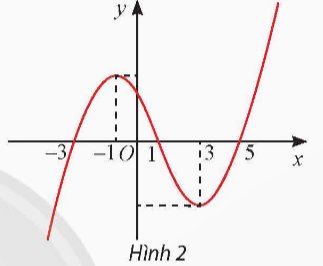
Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng
A. (– 1; 3). B. (– 3; 1).
C. (1; 5). D. (3; + ∞).
Thảo luận (1)Hướng dẫn giảiChọn A
Từ hình vẽ ta thấy, trên khoảng (–1; 3) thì đồ thị hàm số đi xuống nên hàm số nghịch biến
(Trả lời bởi Nguyễn Quốc Đạt)
Giá trị nhỏ nhất của hàm số \(y=\sqrt{x^2+2x+3}\) trên đoạn \(\left[-2;3\right]\) là:
A. \(\sqrt{3}\). B. \(\sqrt{30}\).
C. \(\sqrt{2}\). D. 0.
Thảo luận (1)Hướng dẫn giảiChọn C
Tập xác định: \(D = \mathbb{R}\)
\(y' = \frac{{x + 1}}{{\sqrt {{x^2} + 2x + 3} }} = 0 \Leftrightarrow x = - 1\)
Bảng biến thiên:
Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_D y = y( - 1) = \sqrt 2 \)
(Trả lời bởi Nguyễn Quốc Đạt)
Tiệm cận xiên của đồ thị hàm số \(y=\dfrac{2x^3+3x^2-3}{x^2-1}\) là đường thẳng có phương trình.
A. y = 2x + 3. B. y = 2x + 1.
C. y = x + 3. D. y = x + 1.
Thảo luận (1)Hướng dẫn giảiChọn A
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1;1\} \)
Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } = \frac{{2{x^3} + 3{x^2} - 3}}{{{x^3} - x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^3} + 3{x^2} - 3}}{{{x^3} - x}} = 2\)
\(b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}} - 2x) = 3\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [\frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}} - (2x + 3)] = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x + 3
(Trả lời bởi Nguyễn Quốc Đạt)
Tiệm cận đứng của đồ thị hàm số \(y=\dfrac{-2x+3}{5x+1}\) là đường thẳng có phương trình.
A. y = \(-\dfrac{1}{5}\). B. x = \(-\dfrac{1}{5}\).
C. y = \(-\dfrac{2}{5}\). D. x = \(-\dfrac{2}{5}\).
Thảo luận (1)Hướng dẫn giảiChọn B
Tập xác định: \(D = \mathbb{R}\backslash \{ - \frac{1}{5}\} \)
Ta có: \(\mathop {\lim }\limits_{x \to - {{\frac{1}{5}}^ - }} y = \mathop {\lim }\limits_{x \to - {{\frac{1}{5}}^ - }} \frac{{ - 2x + 3}}{{5x + 1}} = - \infty \), \(\mathop {\lim }\limits_{x \to - {{\frac{1}{5}}^ + }} y = \mathop {\lim }\limits_{x \to - {{\frac{1}{5}}^ + }} \frac{{ - 2x + 3}}{{5x + 1}} = + \infty \)
Vậy đường thẳng x = \( - \frac{1}{5}\) là một tiệm cận đứng của đồ thị hàm số
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số \(y=\dfrac{-2x-3}{4-x}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên (– ∞; – 4) và nghịch biến trên (– 4; + ∞).
B. Hàm số đồng biến trên (– ∞; 4) và (4; + ∞).
C. Hàm số nghịch biến trên (– ∞; 4) và (4; + ∞).
D. Hàm số nghịch biến trên (– ∞; – 4) và (– 4; + ∞).
Thảo luận (1)Hướng dẫn giảiChọn C.
Tập xác định: \(D = \mathbb{R}\backslash \{ 4\} \)
\(y' = \frac{{ - 11}}{{{{(4 - x)}^2}}} < 0\forall x \in D\) nên hàm số luôn nghịch biến trên khoảng (\( - \infty \); 4) và (4; \( + \infty \)).
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm hai số không âm a và b có tổng bằng 10 sao cho:
a) Biểu thức ab đạt giá trị lớn nhất;
b) Tổng các bình phương của chúng đạt giá trị nhỏ nhất;
c) Biểu thức ab2 đạt giá trị lớn nhất.
Thảo luận (1)Hướng dẫn giảiTa có: a, b > 0 và a + b = 10
a) Đặt: \(f(a) = ab = a(10 - a) = - {a^2} + 10a\)
\(f'(a) = - 2a + 10 = 0 \Leftrightarrow a = 5\)
Bảng biến thiên:
Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(5) = 25\)
Vậy để biểu thức ab đạt giá trị lớn nhất là 25 thì a = 5 và b = 5
b) Đặt: \(f(a) = {a^2} + {b^2} = {a^2} + {(10 - a)^2} = 2{a^2} - 20a + 100\)
\(f'(a) = 4a - 20 = 0 \Leftrightarrow a = 5\)
Bảng biến thiên:
Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_{(0; + \infty )} f(a) = f(5) = 50\)
Vậy để biểu thức \({a^2} + {b^2}\) đạt giá trị nhỏ nhất là 50 thì a = 5 và b = 5
c) Đặt: \(f(a) = a{b^2} = a{(10 - a)^2} = {a^3} - 20{a^2} + 100a\)
\(f'(a) = 3{a^2} - 40a + 100 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{10}}{3}\\a = 10\end{array} \right.\)
Bảng biến thiên:
Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(\frac{{10}}{3}) = \frac{{4000}}{{27}}\)
Vậy để biểu thức \(a{b^2}\) đạt giá trị lớn nhất là \(\frac{{4000}}{{27}}\) thì a = \(\frac{{10}}{3}\) và b = \(\frac{{20}}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.
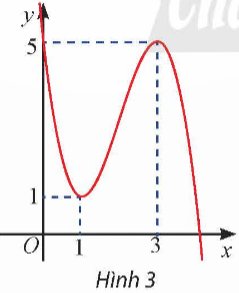
Thảo luận (1)Hướng dẫn giảiHàm số có dạng: \(y = a{x^3} + b{x^2} + cx + d(a < 0)\)
Đồ thị hàm số giao với Oy tại điểm (0; 5) nên: \(y(0) = a{.0^3} + b{.0^2} + c.0 + d = 5 \Leftrightarrow d = 5\)
Đồ thị hàm số đi qua điểm (3; 5) nên: \(y = a{.3^3} + b{.3^2} + c.3 + 5 = 5 \Leftrightarrow 27a + 9b + 3c = 0\)
Đồ thị hàm số đi qua điểm (1; 1) nên: \(y(1) = a{.1^3} + b{.1^2} + c.1 + 5 = 1 \Leftrightarrow a + b + c = - 4\)
Ta có: \(y' = 3a{x^2} + 2bx + c\)
Hàm số đạt cực đại tại điểm (3; 5) nên: \(y'(3) = 3a{x^2} + 2bx + c = 3.a{.3^2} + 2.b.3 + c = 0\)\( \Leftrightarrow 27a + 6b + c = 0\)
Ta có hệ phương trình: \(\left\{ \begin{array}{l}27a + 9b + 3c = 0\\a + b + c = - 4\\27a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 6\\c = - 9\end{array} \right.\)
Vậy hàm số là \(y = - {x^3} + 6{x^2} - 9x + 5\)
(Trả lời bởi Nguyễn Quốc Đạt)