Tìm x, biết:
a) x2 = 10
b) \(\sqrt x = 8\)
c) x3 = - 0,027
d) \(\sqrt[3]{x} = - \frac{2}{3}\)
Tìm x, biết:
a) x2 = 10
b) \(\sqrt x = 8\)
c) x3 = - 0,027
d) \(\sqrt[3]{x} = - \frac{2}{3}\)
Biết rằng 1 < a < 5, rút gọn biểu thức
A = \(\sqrt {{{\left( {a - 1} \right)}^2}} + \sqrt {{{\left( {a - 5} \right)}^2}} \).
Thảo luận (1)Hướng dẫn giảiA = \(\sqrt {{{\left( {a - 1} \right)}^2}} + \sqrt {{{\left( {a - 5} \right)}^2}} \)
\(\begin{array}{l} = \sqrt {{{\left( {a - 1} \right)}^2}} + \sqrt {{{\left( {a - 5} \right)}^2}} \\ = \left| {a - 1} \right| + \left| {a - 5} \right|\\ = a - 1 + 5 - a\\ = 4\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{4 - 2\sqrt 6 }}{{\sqrt {48} }}\)
b) \(\frac{{3 - \sqrt 5 }}{{3 + \sqrt 5 }}\)
c) \(\frac{a}{{a - \sqrt a }}\) với a > 0, a \( \ne \)1
Thảo luận (1)Hướng dẫn giảia) \(\frac{4 - 2\sqrt{6}}{\sqrt{48}} = \frac{2\left(2 - \sqrt{6}\right)}{4\sqrt{3}} = \frac{(2 - \sqrt{6})\sqrt{3}}{2 \cdot (\sqrt{3})^2} = \frac{2\sqrt{3} - 3\sqrt{2}}{6}\)
b) \(\frac{3 - \sqrt{5}}{3 + \sqrt{5}} = \frac{(3 - \sqrt{5})^2}{3^2 - (\sqrt{5})^2} = \frac{14 - 6\sqrt{5}}{4} = \frac{7 - 3\sqrt{5}}{2}\)c) \(\frac{a}{{a - \sqrt a }} = \frac{{a\left( {a + \sqrt a } \right)}}{{\left( {a - \sqrt a } \right)\left( {a + \sqrt a } \right)}} = \frac{{a\left( {a + \sqrt a } \right)}}{{{a^2} - {{\left( {\sqrt a } \right)}^2}}}\)
\( = \frac{{a\left( {a + \sqrt a } \right)}}{{{a^2} - a}} = \frac{{a\left( {a + \sqrt a } \right)}}{{a(a - 1)}} = \frac{{a + \sqrt a }}{{a - 1}}\) với a > 0, a \( \ne \)1
(Trả lời bởi Nguyễn Quốc Đạt)
Biết rằng a > 0, b > 0 và ab = 16. Tính giá trị của biểu thức \(A = a\sqrt {\frac{{12b}}{a}} + b\sqrt {\frac{{3a}}{b}} \).
Thảo luận (1)Hướng dẫn giải\(A =a\sqrt {\frac{{12b}}{a}} + b\sqrt {\frac{{3a}}{b}} = \sqrt {{a^2}\frac{{12b}}{a}} + \sqrt {{b^2}\frac{{3a}}{b}} \\ = \sqrt {12ab} + \sqrt {3ab} = 2\sqrt {3ab} + \sqrt {3ab} = 3\sqrt {3ab}\)
Thay ab = 16 vào ta có:
\(A =3\sqrt {3.16}= 3.4\sqrt {3} = 12\sqrt 3 \)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính \(\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }} - \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\).
Thảo luận (1)Hướng dẫn giải\(\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }} - \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }} = \frac{{{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2} - {{\left( {\sqrt 3 - \sqrt 2 } \right)}^2}}}{{{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\sqrt 2 } \right)}^2}}}\)
\( = \frac{{\left( {\sqrt 3 + \sqrt 2 + \sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 - \sqrt 3 + \sqrt 2 } \right)}}{{3 - 2}}\)
\(\begin{array}{l} = 2\sqrt 3 .2\sqrt 2 \\ = 4\sqrt 6 \end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một trục số được vẽ trên lưới ô vuông như Hình 1.
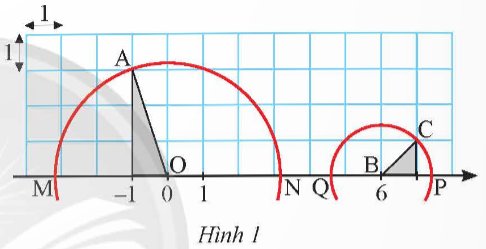
a) Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N. Hai điểm M và N biểu diễn hai số thực nào?
b) Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q. Hai điểm P và Q biểu diễn hai số thực nào?
Thảo luận (1)Hướng dẫn giảia) Ta có OM = OA = \(\sqrt {{1^2} + {3^2}} = \sqrt {10} \) (Áp dụng định lý Pythagore vào tam giác vuông)
Vậy điểm M và N biểu diễn hai số thực lần lượt là - \(\sqrt {10} \) và \(\sqrt {10} \).
b) Ta có BP = BC = \(\sqrt {{1^2} + {1^2}} = \sqrt 2 \) (Áp dụng định lý Pythagore vào tam giác vuông)
Vậy điểm Q và P biểu diễn hai số thực lần lượt là \(6 -\sqrt 2 \) và \(6 + \sqrt 2 \).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp chữ nhật có chiều dài \(\sqrt {12} \)cm, chiều rộng\(\sqrt 8 \)cm, chiều cao \(\sqrt 6 \) như Hình 2.
a) Tính thể tích của hình hộp chữ nhật đó.
b) Tính diện tích xung quanh của hình hộp chữ nhật đó.
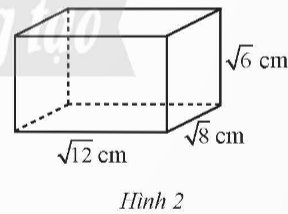
Thảo luận (1)Hướng dẫn giảia) Thể tích của hình hộp chữ nhật đó là:
\(\sqrt {12} \).\(\sqrt 8 \).\(\sqrt 6 \)= \(\sqrt {576} \)= 24 (cm3)
b) Diện tích xung quanh của hình hộp chữ nhật đó là:
2(\(\sqrt {12} \) +\(\sqrt 8 \)).\(\sqrt 6 \)=\(8\sqrt 3 + 12\sqrt 2 \) (cm2).
(Trả lời bởi Nguyễn Quốc Đạt)
Rút gọn các biểu thức sau:
a) \(\left( {a\sqrt {\frac{3}{a}} + 3\sqrt {\frac{a}{3}} + \sqrt {12{a^3}} } \right):\sqrt 3 a\) với a > 0
b) \(\frac{{1 - a}}{{1 + \sqrt a }} + \frac{{1 - a\sqrt a }}{{1 - \sqrt a }}\) với \(a \ge 0;a \ne 1\)
Thảo luận (1)Hướng dẫn giảia) \(\left( {a\sqrt {\frac{3}{a}} + 3\sqrt {\frac{a}{3}} + \sqrt {12{a^3}} } \right):\sqrt 3 a\) với a > 0
\(\begin{array}{l} = \left( {\sqrt {{a^2}.\frac{3}{a}} + \sqrt {{3^2}.\frac{a}{3}} + \sqrt {4.3{a^3}} } \right):\sqrt 3 a\\ = \left( {\sqrt {3a} + \sqrt {3a} + 2a\sqrt {3a} } \right):\sqrt 3 a\\ = \frac{{(2a + 2)\sqrt {3a} }}{{\sqrt 3 a}}\\ = 2a + 2\end{array}\)
b) \(\frac{{1 - a}}{{1 + \sqrt a }} + \frac{{1 - a\sqrt a }}{{1 - \sqrt a }}\) với \(a \ge 0;a \ne 1\)
\( = \frac{{(1 - \sqrt a)(1 + \sqrt a)}}{{1 + \sqrt a }} + \frac{{1 - (\sqrt {a})^3 }}{{1 - \sqrt a }}\\ = 1 - \sqrt a + \frac{{(1 - \sqrt {a})(1 + \sqrt {a} + a )}}{{1 - \sqrt a }} \\= 1 - \sqrt a + 1 + \sqrt {a} + a \\ = 2 + a\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho biểu thức \(P = \left( {\frac{1}{{a + \sqrt a }} - \frac{1}{{\sqrt a + 1}}} \right):\frac{{\sqrt a - 1}}{{a + 2\sqrt a + 1}}\) với a > 0 và a \( \ne \)1.
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi a = 0,25
Thảo luận (1)Hướng dẫn giải\(P = \left( {\frac{1}{{a + \sqrt a }} - \frac{1}{{\sqrt a + 1}}} \right):\frac{{\sqrt a - 1}}{{a + 2\sqrt a + 1}}\)
\( = \left( \frac{1}{ \sqrt a (\sqrt a + 1) } - \frac{1}{\sqrt a + 1}\right) :\frac{{\sqrt a - 1}}{{(\sqrt a + 1) ^2}}\)
\( = \frac{1 - \sqrt a}{{ \sqrt a (\sqrt a + 1) }}.\frac{{(\sqrt a + 1) ^2}}{{\sqrt a - 1}}\)
\( = \frac{ -(\sqrt a - 1)}{{ \sqrt a (\sqrt a + 1) }}.\frac{{(\sqrt a + 1) ^2}}{{\sqrt a - 1}}\)
\( = \frac{-(\sqrt a + 1) }{{ \sqrt a }}\)b) Thay a = 0,25 vào \(P = \frac{-(\sqrt a + 1) }{{ \sqrt a }}\) ta có:
\(P = \frac{-(\sqrt {0,25} + 1) }{{ \sqrt {0,25} }} = \frac{-(0,5 + 1) }{{ 0,5 }} = \frac{-1,5 }{{ 0,5 }} = -3\)
(Trả lời bởi Nguyễn Quốc Đạt)